Глава «Дифференциальное исчисление Функции Нескольких Переменных (ФНП). 1
§1. ФНП-определения. 1
§2. Предел и непрерывность ФНП. 2
§3. Частные производные, производная и градиент ФНП. 4
§4 Дифференцируемость ФНП; формула Тейлора 1 порядка. Касательная плоскость и нормаль к гладкой поверхности z=f(x,y). 5
§5. Производная ФНП по направлению; свойства градиента ФНП в точке. 8
§6.Частные производные высших порядков. Матрица Гессе. 9
§7.Локальные экстремумы ФНП; необходимое условие; стационарные точки. 11
§8 Формула Тейлора 2 порядка для ФНП; достаточное условие локального экстремума гладкой функции двух переменных. 12
§9 Понятие о методе градиентного спуска. 14
«Воспоминания»: Если заданы два
множества ![]() и однозначное соответствие (вило)
f:
и однозначное соответствие (вило)
f: ![]() ,
то
,
то
говорят, что на множестве Df (область определения) задана функция f, значения которой f(d) принадлежат множеству Ef (множество значений),
и пишут: ![]()
Пусть x=![]() »точка»
в “n”-мерном координатном
пространстве и Df={x}
»точка»
в “n”-мерном координатном
пространстве и Df={x}![]()
Определения.
1) Функция ![]() называется «скалярной (числовой)»
функцией “n” переменных.
называется «скалярной (числовой)»
функцией “n” переменных.
Например, f(x,y)=x+xey; f(1,2)=1+1e2; f(2,1)=2(1+e).
2)Функция 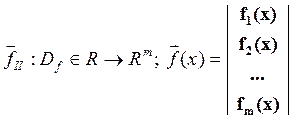 называется
«векторной» функцией одной переменной.
Например,
называется
«векторной» функцией одной переменной.
Например, 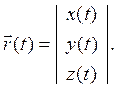
3) Функция 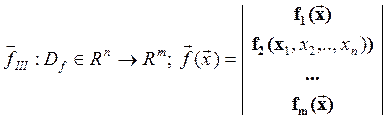 называется «векторной функцией “n” переменных.
называется «векторной функцией “n” переменных.
Например, 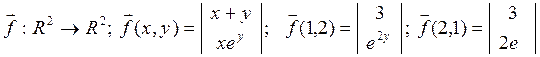
Замечание. Так как функции fII, fIII представляют упорядоченный набор скалярных функций “n”-переменных, в дальнейшем по умолчанию будем рассматривать дифференциальное исчисление скалярной функции “n”-переменных.
3)Суперпозиция ФНП.
«Воспоминания»:
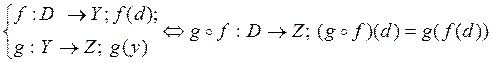
Например,
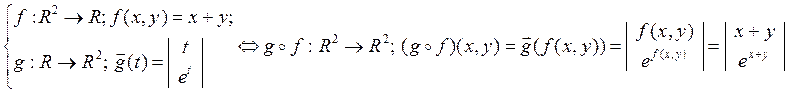
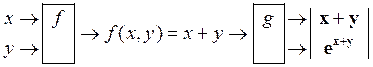
![]()
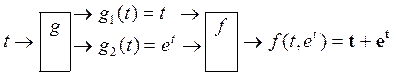
Д/ЗóЭКЗ: определить как суперпозицию функцию f, если f(x,y)=arcsin(x/y)
Пусть ![]() - заданная точка.
- заданная точка.
Окрестность точки a=![]()
- [«открытый шар» в R3; «открытый круг» в R2] радиуса r с центром в точке a; «открытый интервал» ]a-r;a+r[ в R.
Проколотая окрестность точки ПО(a,r)= ![]()
Предельная точка а множества
X={x}: ![]() (любая
ПО точки содержит точки множества !!)
(любая
ПО точки содержит точки множества !!)
Пусть ![]() и
a- предельная точка Df.
и
a- предельная точка Df.
Определение. Число А называется пределом скалярной функции f в точке а,
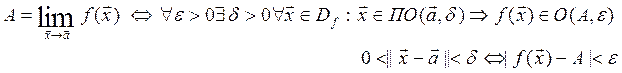
Замечание. Предел функции в точке
существует, если он не зависит от «пути предельного перехода» 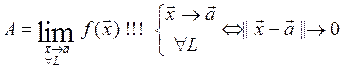
Например, ![]()
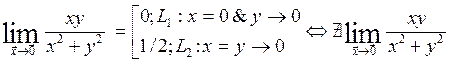
Определение. Функция называется непрерывной в точке а, если
(1)![]() (2)
(2)
![]()
Замечания.
1. элементарные функции непрерывны во внутренних точках области определения.
2. Непрерывная в замкнутой
области Df скалярная функция
принимает в точках области все значения от наименьшего “m” до наибольшего “M”, т.е. Ef=[m;M];![]()
3. «графиком» скалярной функции “n”-переменных называется множество
точек ![]() в “n+1”-мерном координатном пространстве Rn+1:
в “n+1”-мерном координатном пространстве Rn+1:
n=1(ФОП) – линия y=f(x) на плоскости R2;
n=2 – поверхность z=f(x,y) в R3,проекция которой на плоскость ХОУ= Df !!!
4. Из свойств непрерывной функции следует «метод интервалов» решения неравенств f(x,y)<(>)0.
Алгоритм этого метода для n=2.
(1) «Выколоть» на плоскости точки и линии, в которых функция не определена.
(2)Решить уравнение f(x,y)=0 и изобразить соответствующие «нулевые решения» - точки и линии «нулевого уровня» функции на плоскости.
(3)Определить «знак» функции в каждой части плоскости, ограниченной смежными «нулевыми линиями»,- вычислив значение функции в какой-нибудь внутренней точке.
(3)»Срисовать» решение неравенства.
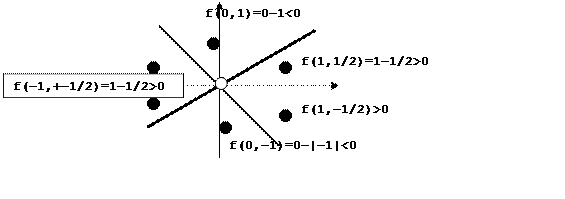 Пример. Решить неравенство
Пример. Решить неравенство 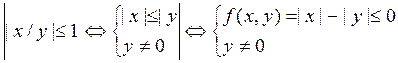
(1)![]() -
прямая на плоскости.
-
прямая на плоскости.
(2)f(x,y)=0ó|x|=|y| ó y=±x
Экз.задача. Изобразить Df на плоскости для функций:
![]()
Пусть функция ![]() непрерывна в точке
непрерывна в точке 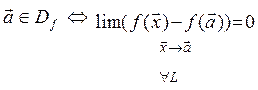 . Зафиксируем все переменные xi=ai; i=1:n; i≠k равными соответствующим
координатам точки а, за исключением ОДНОЙ переменной хк и
рассмотрим функцию ОДНОЙ переменной
. Зафиксируем все переменные xi=ai; i=1:n; i≠k равными соответствующим
координатам точки а, за исключением ОДНОЙ переменной хк и
рассмотрим функцию ОДНОЙ переменной
![]() -сужение функции f на прямую Lk, проходящую через точку а параллельно
«к»-ой координатной оси. Очевидно, что функция
-сужение функции f на прямую Lk, проходящую через точку а параллельно
«к»-ой координатной оси. Очевидно, что функция ![]() непрерывна
в точке «ак».
непрерывна
в точке «ак».
Определение 1. Если в точке «ак»
существует производная ![]() этой ФОП, ее называют частной
производной ФНП f в точке а и пишут:
этой ФОП, ее называют частной
производной ФНП f в точке а и пишут:
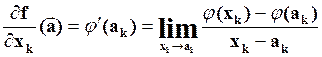 (1)
(1)
Следствия.
1. Аналогично в точке а определены «n» частных производных ФНП.
2. При нахождении частных производных ФНП «работают» правила дифференцирования ФОП.
3. Если ![]() определена в каждой точке
множества
определена в каждой точке
множества ![]() , на множестве Dk определена частная производная
функция «n»
, на множестве Dk определена частная производная
функция «n»
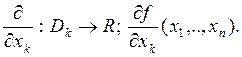
Определение 2. Если в точке ![]() существуют все “n” частных производных,
существуют все “n” частных производных,
- матрица-строка 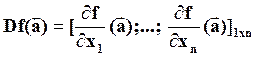 называется производной
функции f в точке а;
называется производной
функции f в точке а;
- вектор ![]() называется
градиентом функции f в точке а
называется
градиентом функции f в точке а
==============================
Пример. f(x,y)=xexy непрерывна в R2 и а=[1;2]t![]()
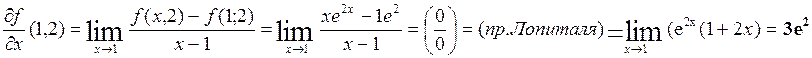
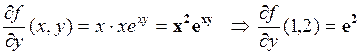 è Df(1;2)=e2[3;1];
è Df(1;2)=e2[3;1]; 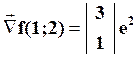
Определение 1. Функция f называется дифференцируемой в точке
непрерывности a=[ax;ay]t, если ее значения в
некоторой окрестности О(x0,r) отличаются от значений
полинома первого порядка на бесконечно малую более высокого порядка малости,
чем 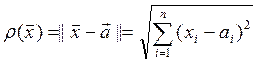 ;
;
Например, для n=2 : 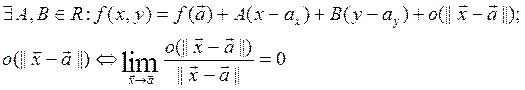
Теорема (без док-ва). Если в точке непрерывности а существуют и непрерывны все частные производные функции f, функция f дифференцируема в точке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.