Комплексные числа. Сопряженные числа. Применение комплексных чисел в геометрии и тригонометрии, страница 4

Теорема 2. Пусть  является корнем уравнения , а - все корни уравнения . Тогда - все корни уравнения .

Доказательство. Эту теорему мы докажем точно так же, как предыдущую. Во-первых,  , т.е. все указанные числа являются корнями этого уравнения. Теперь докажем их попарное неравенство. Пусть для  . Т.к. , мы можем на него сократить. Получим, что , чего быть не может, т.к. мы брали все  корней ой степени из 1, а среди них нет равных. Этим теорема доказана.

Теорема 3. Пусть  является корнем уравнения , а - первообразный корень ой степени из 1. Тогда  - все корни уравнения .

Доказательство. Теорема очевидна. Возьмем ряд   из теоремы 2 и применим к нему теорему 1 ( верно, что ).

Эти три теоремы иногда бывают очень полезны. При больших  нам достаточно вычислить по корню для каждого из уравнений и составить ряд из всех решений для обоих уравнений. К тому же, искать первообразные корни из 1 довольно легко. Это покажет следующая теорема.

Теорема 4. Пусть  - корень уравнения . Тогда 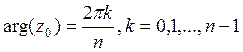.  является первообразным корнем ой степени из 1 в том и только в том случае, если .

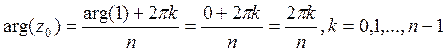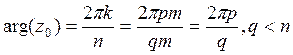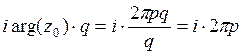Доказательство. . Теперь докажем утверждение о том, что если  является первообразным корнем ой степени из 1, то . Предположим противное, т.е. пусть . Тогда . Тогда имеем . Теперь заметим, что . Высчитаем степень  в этом выражении. . Но мы знаем, что . Теперь видно, что , что противоречит тому, что  - первообразный корень ой степени из 1, т.к. .

Нам осталось доказать следствие в обратную сторону. Докажем, что если , то - первообразный корень ой степени из 1. Доказательство снова будем вести от противного. Предположим, что для некого  выполнено равенство . Преобразуем его. . Последнее утверждение неверно, т.е. мы приходим к противоречию. Этим теорема доказана.

В математике широко распространена функция Эйлера , по которой каждому число сопоставляется количество чисел, меньших его и взаимно-простых с ним (включая единицу). Например, , , . Общая формула функции Эйлера нас сейчас не интересует. Нас интересует следующая, и последняя теорема этого параграфа.

Теорема 5. Уравнение  имеет ровно  первообразных корней.

Доказательство. По предыдущей теореме корень  является первообразным только тогда, когда  в обозначениях предыдущей теоремы. Поскольку каждому такому  соответствует ровно один первообразный корень (это соответствие взаимо-однозначное), то количество первообразных корней равно количеству таких , а их, как несложно понять, .

§7.Неравенство модулей

Как вы, наверное, помните, в свое время у нас было несколько неравенств для модулей вещественных чисел. Интересно, что эти неравенства сохраняются и для комплексных чисел.

Лемма.

Теорема 1.

Доказательство. Докажем сначала неравенство . Сделаем мы это алгебраическим способом. Положим . Тогда    . Как мы знаем, . Воспользуемся этим неравенством. . Что и требовалось доказать. Теперь возьмем  и подставим в только что доказанное неравенство. Получим . Этим доказана теорема целиком.

Теорема 2.

Доказательство. Доказательство снова проведем алгебраически. Как мы уже знаем из предыдущей задачи (обозначения сохраняются), . Мы также знаем, что , поэтому . Последнее выражение и дает требуемое неравенство. Подставляя , получаем вторую часть неравенства. Теорема доказана.

В качестве комментария добавлю, что последняя теорема очень легко доказывается геометрически.