Комплексные числа. Сопряженные числа. Применение комплексных чисел в геометрии и тригонометрии

Комплексные числа

§1. Основные определения

Def. Рассмотрим множество пар вещественных чисел. Зададим на нем два действия и равенство. . . . Такое множество с вот так заданными равенством и операциями называется множеством комплексных чисел и обозначается .

Свойства комплексных чисел

1)   (коммутативность сложения)

2)  (ассоциативность сложения)

3)   (нейтральный элемент по сложению)

4)   (обратный по сложению элемент)

5)   (коммутативность умножения)

6)   (ассоциативность умножения)

7)   (нейтральный элемент по умножению)

8)   (обратный по умножению элемент)

9)   (дистрибутивность)

Доказательства свойств

1) 

2)   

3)  Рассмотрим пару . Она, очевидно, удовлетворяет условию. Пусть есть еще одна пара , удовлетворяющая условию. Тогда . Но в этом случае . Свойство доказано.

4)   Свойство доказано.

5) 

6)  Два выражения равные в силу коммутативности сложения вещественных чисел. Свойство доказано.

7)  Очевидно, что пара  удовлетворяют условию. Пусть еще какая-то пара  удовлетворяет условию. Тогда . Свойство доказано.

8)  Во-первых, докажем единственность такого элемента. Пусть таких элемента два. Пусть это пары  и . Тогда  . Теперь осталось найти этот обратный элемент.  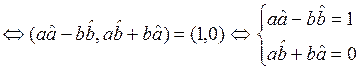 Из этой системы надо выразить  и  через  и . Сначала домножим первое уравнение на , а второе на , и сложим эти уравнения. Получим 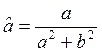. Аналогично 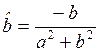. Таким образом, это свойство доказано.

9)   

Нашей следующей целью будет согласование вещественных чисел с комплексными. Вещественному числу  сопоставим пару . Такое отображение корректно, поскольку  и . Теперь мы видим, что операции  и  корректны и на вещественных числах, поэтому их мы будем далее обозначать, как обычно, + и .

Обозначим пару  за . Тогда . Очевидно так же, что . Такая форма записи комплексных чисел называется алгебраической. Ею обычно пользуется в литературе, хотя редко поясняют, откуда она взялась и что это за магическое , которое еще иногда обозначают как корень из -1. При такой записи, кстати,  называется вещественной частью и обозначается ,  - мнимой частью (), а  называется модулем числа и обозначается . Очень важно, что вещественная и мнимая части числа, а так же его модуль являются вещественными числами.

Теперь введем вычитание и деление комплексных чисел.

Def. Разностью чисел  и  назовем сумму  и числа, обратного к  по сложению.

Def. Частным от деления  на  назовем произведение  и числа, обратного к  по умножению. Деление на вещественный ноль (пару (0,0)) не определено.

Th. .

Доказательство.

Th.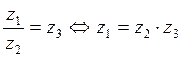

Доказательство.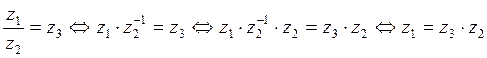

В последней теореме через  обозначается элемент, обратный к  по умножению. Вообще со степенями в комплексных числах все очень просто: их можно возводить только в степень с целым показателем. Из комплексных чисел нельзя извлекать корни, поэтому уже рациональная степень не определена. Дадим точное определение степени.

Def. Пусть . Тогда .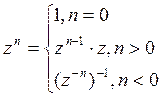

Все обычные свойства степени при этом сохраняются, и их несложно доказать. Подробнее о степенях будет рассказано в §4.

§2. Сопряженные числа

Def. Сопряженным с числом  называется число . Обозначается сопряженное как , т.е. .

Свойства сопряженных чисел

1) 

2) 

3) 

4) 

5) 

6) 

7) 

Доказательства

Далее в некоторых свойствах

1) 

2) 

3) 

4)  Аналогично третьему, и так же очевидно

5) 

6) 

7) 

Теперь еще немного о делении. Заметим, что 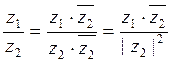. Таким образом, деление комплексных чисел мы умеем записывать как деление комплексного числа на вещественное число. Вообще во всевозможных дробях не принято оставлять комплексные числа в знаменателе. Теперь вы знаете, как избавиться от «комплексности» в знаменателе.

На этом обзор сопряженных чисел закончен. Теперь перейдем к самому интересному в комплексных числах – геометрии.

§3. Геометрическая интерпретация и тригонометрическая форма записи

Рассмотрим плоскость с декартовой системой координат. Комплексному числу  сопоставим точку с координатами . При этом само число можно рассматривать как вектор. Расстояние от точки до начала координат, т.е. длина вектора, это по теореме Пифагора не что иное как модуль нашего числа. Наше определение модуля, кстати, сохраняется и для вещественных чисел. Также наш вектор вместе с вещественной прямой образуют некий угол. Для каждого комплексного числа его расстояние до начала координат и его угол однозначны. Угол, образуемый данным числом с вещественной осью, называется аргументом данного числа (обозначается ).

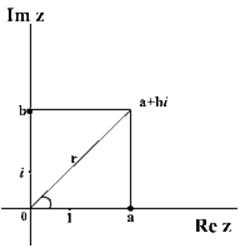Из рисунка слева мы видим, что если  и , то . Тогда само . Такая форма записи комплексного числа называется тригонометрической. Для каждого числа она, очевидно, единственна. Поскольку комплексные числа очень тесно связаны с геометрией на плоскости, эта форма записи нам еще не раз пригодится.