Комплексные числа. Сопряженные числа. Применение комплексных чисел в геометрии и тригонометрии, страница 2

Но пока отметим еще один интересный факт. Заметим, что если , то . Таким образом, сопряженные числа симметричны относительно вещественной оси.

Теперь давайте попробуем попереводить комплексные числа из одной формы записи в другую. Перевод из тригонометрической формы в алгебраическую предельно прост: надо посчитать значения соответствующих тригонометрических функций и подставить их. Перевод из алгебраической формы в тригонометрическую также несложен. 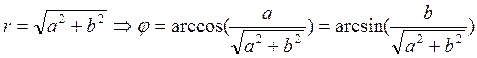 . Например, переведем число  в тригонометрическую форму. . Тогда . В итоге . Из двух вариантов записи углов предпочтительней радианный. Приведем еще несколько популярных примеров:

1) 

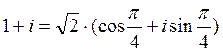
2) 

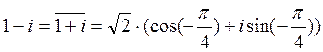
3) 

4) 

5) 

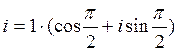
Теперь докажем полезную теорему об умножении и делении комплексных чисел в тригонометрической форме.

Th.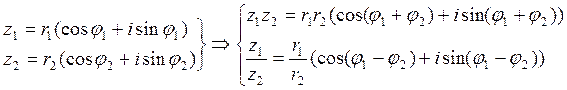

Доказательство.   , что и требовалось доказать. Часть про деление доказывается точно так же.

Докажем формулу Муавра.

Th. , где  - целое число.

Доказательство. Для  формула очевидно верна, т.к. обе части равенства обращаются в единицу. Теперь проведем индукцию по показателю степени. Пусть формула верна для некого . Тогда по предыдущей теореме имеем . Таким образом, мы доказали теорему для натурального . Для целого достаточно доказать переход от  к . Это делается точно так же. Поэтому можно считать формулу доказанной.

Из первой теоремы можно вывести несколько полезных геометрических свойств. Например, если отношение двух комплексных чисел равно , то два соответствующих вектора перпендикулярны и равны по длине. Если , где - вещественное, то вектор  перпендикулярен и в  раз длиннее его. Напомню, что для перпендикулярности векторов достаточно, чтобы аргументы соответствующих им чисел отличались на . В двух наших случаях это вытекает из теоремы о делении и умножении (из нашей первой теоремы).

На сем данный параграф заканчивается, но к геометрии комплексных чисел мы еще вернемся.

§4. Показательная форма записи

В тригонометрической форме записи есть одно неудобство: она слишком длинная. Введем новое обозначение.  будем обозначать как . Вопрос о том, что здесь делает Эйлерово число, оставим на потом. Наше переобозначение теперь позволяет записать комплексное число в виде  . Такая форма записи называется показательной. Удобства такой формы записи заключены в следующих свойствах:

1) 

2) 

3)  , где - целое число.

4)  , где - целое число.

Все эти свойства вытекают из теорем для тригонометрической формы записи. Тем не менее, показательная форма очень часто используется, особенно в тех задачах, где приходится очень много умножать и возводить в степень комплексные числа. Скажем, возводить  в десятую степень сложно, зато куда проще посчитать  . Повторю, что все свойства степени с целым показателем сохраняются и для показательной формы записи комплексных чисел. Перевод в показательную форму из алгебраической и наоборот выполняется через тригонометрическую. Как это делать, написано в предыдущем параграфе.

§5. Решение уравнений в комплексных числах

Начнем с самого простого – линейного уравнения с комплексными коэффициентами и одним неизвестным. Далее - комплексные коэффициенты в уравнениях, - натуральное число, - целые числа, а - неизвестные.

Итак, рассмотрим уравнение . Решается оно точно так же, как и вещественное, т.е. 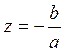. Теперь перейдем к системе из двух линейных уравнений с двумя неизвестными. Для нее решение тоже такое же, как и в вещественных чисел. Да и вообще все уравнения первой степени в комплексных числах решаются точно так же, как и в вещественных. Исключения составляют те уравнения для решения которых приходится пользоваться понятиями, не определенными для комплексных чисел, например, извлечение корня, разложение в цепную дробь, нахождение общего делителя и так далее. Такие случаи надо разбирать отдельно. Здесь мы разберем два таких случая.