Аналогично, из прямоугольного
треугольника ![]() соответствующего
геометрическому расположению точек при рабочем положении захватного рычага,
находим угол b2
соответствующего
геометрическому расположению точек при рабочем положении захватного рычага,
находим угол b2
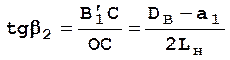 .
(2.45)
.
(2.45)
Отсюда получаем
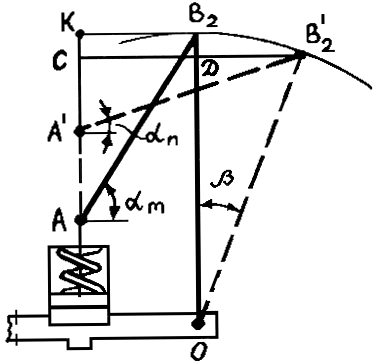 |
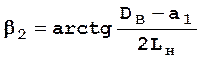 . (2.46)
. (2.46)
Теперь, когда определили углы ![]() и
и ![]() можно
определить угол
можно
определить угол ![]() поворота захватных рычагов
поворота захватных рычагов
![]() . (2.47)
. (2.47)
Для определения хода hш поршня пневмопривода и длины l распорных рычагов рассмотрим геометрическое положение внутреннего конца захватного рычага при рабочем и исходном положениях относительно точки 0 его поворота. В результате получим плоские геометрические фигуры, где заданы:
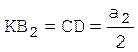 ,
, ![]() ,
,
![]() , (рис. 2.9)
, (рис. 2.9)
В прямоугольном треугольнике ![]() определим
длину противолежащего катета
определим
длину противолежащего катета ![]()
![]() . (2.48)
. (2.48)
Тогда в прямоугольном треугольнике ![]() определим длину
гипотенузы
определим длину
гипотенузы ![]() , которая
соответствует длине l
распорного
рычага
, которая
соответствует длине l
распорного
рычага
- 26 -
![]() l
l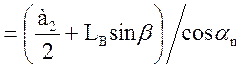 , (2.49)
, (2.49)
и далее определяем длину противолежащего катета
![]() l
l![]() . (2.50)
. (2.50)
Рис. 2.9. Схема к расчету хода hш поршня и длины l распорных рычагов
Переходим к определению угла am наклона распорных рычагов при исходном положении кинематических звеньев, который заключен в прямоугольном треугольнике АКВ2
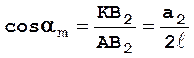 . (2.51)
. (2.51)
Отсюда получаем
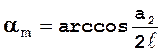 . (2.52)
. (2.52)
- 27 –
Далее определяем длину противолежащего катета
![]() l
l![]() . (2.53)
. (2.53)
Прямая, заключенная между точками D и В2 является
высотой сегмента с центральным углом 2b, длина дуги которого
соответствует траектории движения шарнирного соединения захватного и распорного
рычагов по окружности, с радиусом![]() . По известной формуле определим
высоту сегмента:
. По известной формуле определим
высоту сегмента:
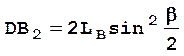 . (2.54)
. (2.54)
Теперь нетрудно определить ход hш -поршня пневмопривода, соответствующего длине отрезка А'А катета АК.
![]() . (2.55)
. (2.55)
Подставляя (2.50), (2.53) и (2.54) в (2.55), окончательно запишем
![]() l
l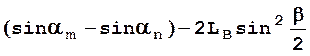 , (2.56)
, (2.56)
Таким образом, рассмотрена методика расчета параметров манипуляционной системы захватной головки, из множества которых выделим P2, DT, hш, и Fo являющихся исходными данными для расчета возвратной пружины пневмопривода.
2.4. Алгоритм расчета манипуляционной системы на ПЭВМ
Расчет манипуляционной системы захватной головки по изложенной методике с помощью точных алгебраических уравнений в установленной последовательности относительно параметров
-28-
bM, DT, b и l не представляется возможным. Тогда примем метод последовательных приближений (метод повторных подстановок), где количество циклов вычислений зависит от точности расчета диаметра DTпневмоцилиндра.
Для выполнения расчетов по методу последовательных приближений с применением ПЭВМ разработана блок-схема (рис. 2.10), где приведены основные формулы, их номер и пояснения по организации процесса вычисления. В блок-схеме исходные данные представлены в интервале численных значений, что позволяет формировать различные варианты параметров манипуляционной системы захватной головки.
Начало
 |
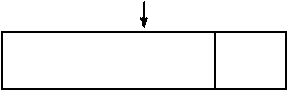
Вод исходных данных
![]()
 |
![]()
 |
![]()
Рис. 2.10. Блок-схема алгоритма расчета
манипуляционной системы
- 29 -
![]()
|
|
|
![]()
 |
![]()
 |
![]()
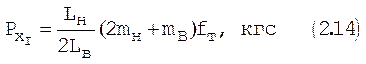
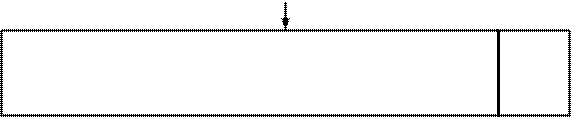 |
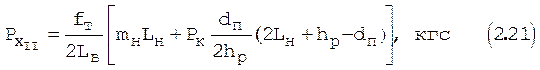


|


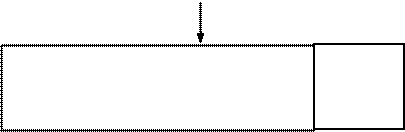
![]()
![]() , кгс
, кгс


![]()
![]()
![]()
![]()
![]() На первом шаге расчета(2.3)
На первом шаге расчета(2.3)
принять F0=0
1 2
Продолжение рис. 2.10.
- 30 –
![]()
![]()
![]() 1 2
1 2
![]()
![]()

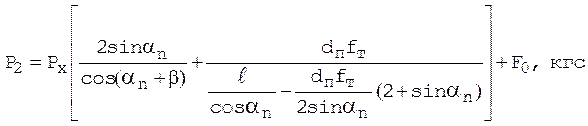
![]() На первом шаге расчета принять
На первом шаге расчета принять
![]() (2.27) .
(2.27) .
![]()
 |
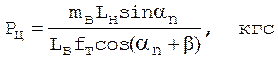
На первом шаге расчета принять (2.32)
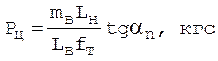
 |
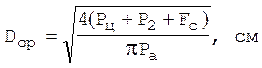
На первом шаге расчета (2.35) принять Fc=0
 |
![]() Печать
Печать
![]()
 |
Из табл. 5.1 относительно
диаметра ![]() выбрать и
выбрать и
ввести ![]() , см
, см
![]()
![]()
![]() 1 2
1 2
Продолжение рис. 2.10.
- 31 –
![]()
![]()
![]() 1 2
1 2


![]()
![]()
![]()
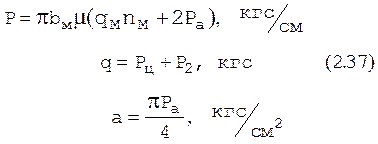
 |

 (2.38)
(2.38)
 |
|


 |
![]() Печать
Печать
![]()
 |
Из табл. 5.1 относительно
диаметра ![]() по условию
по условию
![]() (2.40)
(2.40)
выбрать и
ввести ![]() , см
, см
![]()
![]()
![]()
1 2
Продолжение рис. 2.10.
- 32 –
![]()
![]()
![]() 1 2
1 2
![]()
![]()



![]()
![]()
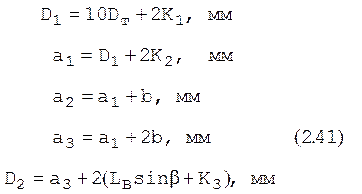
На первом шаге расчета
принять ![]() , мм
, мм
 |
 |
 |
![]()
 |
l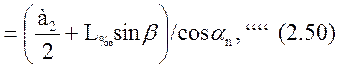


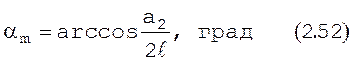
![]()
![]()
![]()
1 2
Продолжение рис. 2.10.
- 33 –
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.