Министерство
образования Российской федерации
Государственное образовательное учреждение
высшего
профессионального образования
«Сибирский государственный индустриальный университет»
Кафедра
металлургии и технологии сварочного производства
ОЦЕНКА ДИСПЕРСИИ
В ЗАДАЧАХ
СТАТИСТИЧЕСКОГО
КОНТРОЛЯ КАЧЕСТВА
Методические
рекомендации
к выполнению
практической работы по курсу
«Статистические методы
управления качеством»
для студентов
специальности «Управление качеством» (340100)
Новокузнецк 2003
УДК 658.56
Рецензент
Кандидат технических наук, доцент кафедры
электрометаллургии, стандартизации и сертификации ГОУ ВПО «СибГИУ»
Оценка дисперсии в задачах статистического
контроля качества: Метод. рек. /Сост.: Ю.Г. Сильвестров: ГОУ ВПО «СибГИУ».
- Новокузнецк, 2003, -
11 с.
Изложены
общие теоретические положения проверки гипотез о дисперсиях нормально
распределенных генеральных совокупностей в задачах статистического контроля
качества. Разобраны практические примеры. Даны задачи для самостоятельного
решения.
Предназначены
для студентов специальности «Управление качеством» (340100)
по курсу «Статистические методы управления качеством».
1. ЦЕЛЬ РАБОТЫ
1.1.
Ознакомиться с основными теоретическими положениями о проверки
гипотез о дисперсиях нормально распределенных генеральных совокупностей.
1.2.
Закрепить полученные знания при решении практических задач.
2. Проверка гипотезы о дисперсии нормально
распределенной генеральной совокупности.
Методы проверки дисперсии имеют особую важность
при анализе точности и стабильности технологических процессов,
измерительных приборов и станков.
Пусть на основании предшествующих опытных данных
контроля деталей, обрабатываемых на станке, известно, что величины их
диаметра имеют нормальное распределение со стандартным отклонением 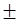 20 20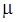 км ( км (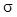 2=400 2=400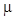 км2). км2).
С целью
проверки постоянства настройки станка берется выборка объемом n=20 и рассчитываются ее статические характеристики:
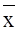 = 20 мм; S2 = 841 = 20 мм; S2 = 841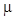 км2; S = 29 км2; S = 29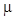 км. км.
Можно ли на основании этих
результатов заключить, что станок настроен как обычно, или величина S = 29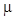 км
говорит о несоответствии станка предъявляемым требованиям. км
говорит о несоответствии станка предъявляемым требованиям.
Последовательность решения такой задачи выглядит
следующим образом. Предполагают, что выборка взята из генеральной
совокупности с 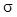 0
= 20 0
= 20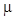 км, т.е.
проверяемая гипотеза гласит: Н0: км, т.е.
проверяемая гипотеза гласит: Н0: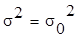 . Эту гипотезу
проверяют по выборочной характеристике . Эту гипотезу
проверяют по выборочной характеристике 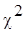 (кси –квадрат) : (кси –квадрат) :
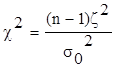 ,
(1) ,
(1)
которая удовлетворяет 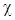 2
распределению с m = n – 1
степенями свободы, если гипотеза Н0 верна. 2
распределению с m = n – 1
степенями свободы, если гипотеза Н0 верна.
При
вероятности ошибки 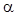 критическое
значение критическое
значение 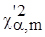 определяют из
соотношения : определяют из
соотношения :
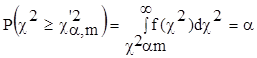 ,
(2) ,
(2)
где 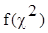 -
плотность -
плотность 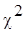 распределения: распределения:
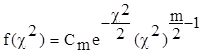 ,
(3) ,
(3)
где Сm - постоянная,
значение которой зависит только от m.
Критическая
область – область непринятия гипотезы Н0 определяется
неравенством:
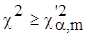 .
(4) .
(4)
Величина 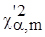 находится
по известным находится
по известным 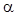 и m из таблицы 1 в приложении. Для принятой гипотезы
находим: и m из таблицы 1 в приложении. Для принятой гипотезы
находим:
 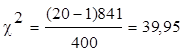 . .
Пусть 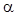 = 0,01. Тогда по
таблице 1 из приложения находим = 0,01. Тогда по
таблице 1 из приложения находим 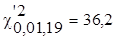 .
Ввиду того, что .
Ввиду того, что 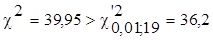 ,
гипотеза Н0 отвергается. Станок не обеспечивает требуемой
точности. ,
гипотеза Н0 отвергается. Станок не обеспечивает требуемой
точности.
3. Проверка гипотезы о значениях двух
дисперсий
из нормально распределенных генеральных
совокупностей.
Пусть
имеются две независимые выборки объемом n1
и n2 из двух нормально распределенных
генеральных совокупностей. Их статистические характеристики равны
соответственно :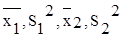 .
Необходимо проверить предположение, что генеральные совокупности имеют
одинаковые дисперсии: .
Необходимо проверить предположение, что генеральные совокупности имеют
одинаковые дисперсии: 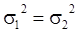 . .
Для
проверки гипотезы Н0 : 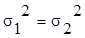 используют выборочную
характеристику: используют выборочную
характеристику:
F
=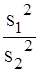 ,
(5) ,
(5)
которая соответствует F распределению Фишера с m1
= n1 – 1 cтепенями
свободы. Плотность F распределения записывается
следующим образом:
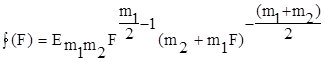 , (6) , (6)
где 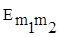 зависит лишь от m1 и m2. зависит лишь от m1 и m2.
При
вероятности ошибки 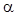 практическое
значение F` практическое
значение F`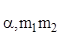 определяется из
соотношения: определяется из
соотношения:
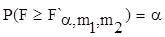 (7)
(7)
При
расчете F в числителе должна стоять большая по
величине выборочная дисперсия. Значение 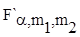 для данных для данных 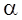 и (m1,m2)
степеней свободы находятся по таблице 2 и 3 в приложении. и (m1,m2)
степеней свободы находятся по таблице 2 и 3 в приложении.
Метод
проверки гипотезы Н0 : 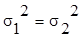 , т.к. «F – критерий» формулируется так: при F = , т.к. «F – критерий» формулируется так: при F = 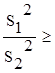 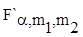 гипотеза
Н0 отвергается, т.к. расхождение между выборочными дисперсиями
являются значимыми. В случае F< гипотеза
Н0 отвергается, т.к. расхождение между выборочными дисперсиями
являются значимыми. В случае F<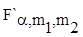 - гипотеза принимается. - гипотеза принимается.
4. Задачи.
1.
На рабочем месте выборочно проводится хронометраж и фиксируется
время выполнения рабочим определенной операции с целью сделать выводы о
равномерности его работы. При выборке объема n = 9 вычислены статистические характеристики: 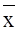 = 83 мин., S2 = 4.04 мин.2 Мерой
равномерности работы можно считать дисперсию S2. = 83 мин., S2 = 4.04 мин.2 Мерой
равномерности работы можно считать дисперсию S2.
Необходимо проверить, существенно ли отличается дисперсия 4.04 мин.2
данного рабочего от дисперсии S2 =
3мин.2, рассчитанной на основании большого числа измерений
продолжительности одной и той же операции. Вероятность ошибки возьмите
равной 0.05.
2.
Точность работы станка–автомата проверяется по дисперсии
контролируемого размера изделий, которая не должна превышать 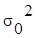 =0,1. Взята проба
из 25 случайных отобранных изделий, по результатам измерений которых
получены следующие данные: =0,1. Взята проба
из 25 случайных отобранных изделий, по результатам измерений которых
получены следующие данные:
|
Контролируемый
размер, хi
|
3.0
|
3.5
|
3.8
|
4.4
|
4.5
|
|
Частота, hi
|
2
|
6
|
9
|
7
|
1
|
Требуется при уровне значимости 0.05 проверить, обеспечивает ли
станок требуемую точность.
3.
Из нормальной генеральной совокупности деталей извлечена выборка объемом
n = 21 и по ней найдена
дисперсия контролируемого параметра S2=16,2.
Требуется при уровне значимости 0,01 проверить нулевую гипотезу H0 : 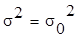 = 15. = 15.
4.
При оценке индекса возможности процесса обработки деталей на станке
исходят из дисперсии, равной 0,18. При очередном контроле технологического
процесса была взята выборка объемом n = 31 и
получены следующие результаты измерений:
|
хi
|
10,1
|
10,3
|
10,6
|
11,2
|
11,5
|
11,8
|
12,0
|
|
hi
|
1
|
3
|
7
|
10
|
6
|
3
|
1
|
Исходя из уровня
значимости 0,05, оцените, соответствует ли технологический процесс
требуемому уровню точности.
5.
Из нормальной генеральной совокупности извлечена выборка объемом n = 8 и по ней найдена дисперсия
S = 0.25.
Проверьте нулевую гипотезу 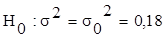 при уровне
значимости 0,05. при уровне
значимости 0,05.
6.
Для проверки точности двух шлифовальных станков проведены измерения
толщины обрабатываемых на них одинаковых деталей. По результатам n1 = 25 измерений деталей со станка №1 получено
стандартное отклонение S1 = 7,98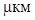 , а по
результатам n2 = 30 измерений деталей со станка №2
–S2 = 5,71 , а по
результатам n2 = 30 измерений деталей со станка №2
–S2 = 5,71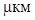 . .
Можно ли на основании этих результатов при вероятности ошибки 0,05 сказать,
что точность станка №2 выше точности станка №1?
7.
Для сравнения удельного веса кирпичей из двух зон обжига печи (А и
В) отобрали и взвесили n1 = 14 кирпичей из зоны А и n2 = 10 кирпичей из зоны В. Обработка результатов
взвешивания дала следующие значения дисперсий : S12
= 16,4 (кг/м3)2 для зоны А и S22
= 22,5 (кг/м3)2 для зоны В.
Следует ли на основании этих результатов при уровне значимости 0,05
говорить, что разброс удельных весов кирпичей не зависит от зоны их обжига в
печи.
8.
Производилось сравнение точности химического анализа у двух лаборантов,
один из которых (А) был новичком в работе, а другой (В) опытным работником.
Лаборант А выполнил 20 анализов, а лаборант В - 13 анализов одного и того
же вещества. Обработка результатов этих анализов дала следующие значения
статистических характеристик:
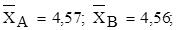 ЅА2 =
0,0295; ЅВ2
= 0,0139. ЅА2 =
0,0295; ЅВ2
= 0,0139.
Оцените
профессиональные качества новичка, взяв в качестве уровня значимости 0,05.
9.
Для сравнения точности двух станков-автоматов взяты две выборки,
объемы которых n1 = 10 и n2 = 8. По результатам
измерений деталей выборки получены следующие данные:
|
Станок №1
|
1,08
|
1,10
|
1,12
|
1,14
|
1,15
|
1.25
|
1,36
|
1,38
|
1.40
|
1,42
|
|
Станок №2
|
1.11
|
1,12
|
1,18
|
1,22
|
1,33
|
1.35
|
1,36
|
1.38
|
|
|
Можно ли считать,
что станки обладают одинаковой точностью при вероятности ошибки 0,01.
ПРИЛОЖЕНИЕ А
Значения 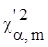 для
различных для
различных 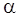 и m и m
|
Число степеней
свободы,
m
|
Уровень
значимости 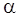
|
|
0,1
|
0,05
|
0,01
|
|
1
|
2,71
|
3,84
|
6,63
|
|
2
|
4,61
|
5,99
|
9,21
|
|
3
|
6,25
|
7,81
|
11,3
|
|
4
|
7,78
|
9,49
|
13,3
|
|
5
|
9,24
|
11,1
|
15,1
|
|
6
|
10,6
|
12,6
|
16,8
|
|
7
|
12,0
|
14,1
|
18,5
|
|
8
|
13,4
|
15,5
|
20,1
|
|
9
|
14,7
|
16,9
|
21,7
|
|
10
|
16,0
|
18,3
|
23,2
|
|
11
|
17,3
|
19,7
|
24,7
|
|
12
|
18,5
|
21,0
|
26,2
|
|
13
|
19,8
|
22,4
|
27,7
|
|
14
|
21,1
|
23,7
|
29,1
|
|
15
|
22,3
|
25,0
|
30,6
|
|
16
|
23,5
|
26,3
|
32,0
|
|
17
|
24,8
|
27,6
|
33,4
|
|
18
|
26,0
|
28,9
|
34,8
|
|
19
|
27,2
|
30,1
|
36,2
|
|
20
|
28,4
|
31,4
|
37,6
|
|
21
|
29,6
|
32,7
|
38,9
|
|
22
|
30,8
|
33,9
|
40,3
|
|
23
|
32,0
|
35,2
|
41,6
|
|
24
|
33,2
|
36,4
|
43,0
|
|
25
|
34,4
|
37,7
|
44,3
|
|
26
|
35,6
|
38,9
|
45,0
|
|
27
|
36,7
|
40,1
|
47,0
|
|
28
|
37,9
|
41,3
|
48,3
|
|
29
|
39,1
|
42,6
|
49,6
|
|
30
|
40,3
|
43,8
|
50,9
|
ПРИЛОЖЕНИЕ
В
Значение F при Р = 0,05
|

|
1
|
2
|
3
|
4
|
5
|
6
|
8
|
12
|
24
|
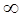
|
|
1
|
161,4
|
199,5
|
215,7
|
224,6
|
230,2
|
234,0
|
238,9
|
243,9
|
249,0
|
254,3
|
|
2
|
18,51
|
19,00
|
19,16
|
19,25
|
19,30
|
19,33
|
19,37
|
19,41
|
19,45
|
19,50
|
|
3
|
10,13
|
9,55
|
9,28
|
9,12
|
9,01
|
8,94
|
8,84
|
8,74
|
8,64
|
8,53
|
|
4
|
7,71
|
6,94
|
6,59
|
6,39
|
6,26
|
6,16
|
6,04
|
5,91
|
5,77
|
5,63
|
|
5
|
6,61
|
5,79
|
5,41
|
5,19
|
5,05
|
4,95
|
4,82
|
4,68
|
4,53
|
4,36
|
|
6
|
5,99
|
5,14
|
4,76
|
4,53
|
4,39
|
4,28
|
4,15
|
4,00
|
3,84
|
3,67
|
|
7
|
5,59
|
4,74
|
4,35
|
4,12
|
3,97
|
3,87
|
3,73
|
3,57
|
3,41
|
3,23
|
|
8
|
5,32
|
4,46
|
4,07
|
3,84
|
3,69
|
3,58
|
3,44
|
3,28
|
3,12
|
2,93
|
|
9
|
5,12
|
4,26
|
3,86
|
3,63
|
3,48
|
3,37
|
3,23
|
3,07
|
2,90
|
2,71
|
|
10
|
4,96
|
4,10
|
3,71
|
3,48
|
3,33
|
3,22
|
3,07
|
2,91
|
2,74
|
2,54
|
|
11
|
4,84
|
3,98
|
3,59
|
3,36
|
3,20
|
3,09
|
2,95
|
2,79
|
2,61
|
2,40
|
|
12
|
4,75
|
3,88
|
3,49
|
3,26
|
3,11
|
3,00
|
2,85
|
2,69
|
2,50
|
2,30
|
|
13
|
4,67
|
3,80
|
3,41
|
3,18
|
3,02
|
2,92
|
2,77
|
2,60
|
2,42
|
2,21
|
|
14
|
4,60
|
3,74
|
3,34
|
3,11
|
2,96
|
2,85
|
2,70
|
2,53
|
2,35
|
2,13
|
|
15
|
4,54
|
3,68
|
3,29
|
3,06
|
2,90
|
2,79
|
2,64
|
2,48
|
2,29
|
2,07
|
|
16
|
4,49
|
3,63
|
3,24
|
3,01
|
2,85
|
2,74
|
2,59
|
2,42
|
2,24
|
2,01
|
|
17
|
4,45
|
3,59
|
3,20
|
2,96
|
2,81
|
2,70
|
2,55
|
2,38
|
2,19
|
1,96
|
|
18
|
4,41
|
3,55
|
3,16
|
2,93
|
2,77
|
2,66
|
2,51
|
2,34
|
2,15
|
1,92
|
|
19
|
4,38
|
3,52
|
3,13
|
2,90
|
2,74
|
2,63
|
2,48
|
2,31
|
2,11
|
1,88
|
|
20
|
4,35
|
3,49
|
3,10
|
2,87
|
2,71
|
2,60
|
2,45
|
2,28
|
2,08
|
1,84
|
|
21
|
4,32
|
3,47
|
3,07
|
2,84
|
2,68
|
2,57
|
2,42
|
2,25
|
2,05
|
1,81
|
|
22
|
4,30
|
3,44
|
3,05
|
2,82
|
2,66
|
2,55
|
2,40
|
2,23
|
2,03
|
1,78
|
|
23
|
4,28
|
3,42
|
3,03
|
2,80
|
2,64
|
2,53
|
2,38
|
2,20
|
2,00
|
1,76
|
|
24
|
4,26
|
3,40
|
3,01
|
2,78
|
2,62
|
2,51
|
2,36
|
2,18
|
1,98
|
1,73
|
|
25
|
4,24
|
3,38
|
2,99
|
2,76
|
2,60
|
2,49
|
2,34
|
2,16
|
1,96
|
1,71
|
|
26
|
4,22
|
3,37
|
2,98
|
2,74
|
2,59
|
2,47
|
2,32
|
2,15
|
1,95
|
1,69
|
|
27
|
4,21
|
3,35
|
2,96
|
2,73
|
2,57
|
2,46
|
2,30
|
2,13
|
1,93
|
1,67
|
|
28
|
4,20
|
3,34
|
2,95
|
2,71
|
2,56
|
2,44
|
2,29
|
2,12
|
1,91
|
1,65
|
|
29
|
4,18
|
3,33
|
2,93
|
2,70
|
2,54
|
2,43
|
2,28
|
2,10
|
1,90
|
1,64
|
|
30
|
4,17
|
3,32
|
2,92
|
2,69
|
2,53
|
2,42
|
2,27
|
2,09
|
1,89
|
1,62
|
|
40
|
4,08
|
3,23
|
2,84
|
2,61
|
2,45
|
2,34
|
2,18
|
2,00
|
1,79
|
1,52
|
|
60
|
4,00
|
3,15
|
2,76
|
2,52
|
2,37
|
2,25
|
2,10
|
1,92
|
1,70
|
1,39
|
|
120
|
3,92
|
3,07
|
2,68
|
2,45
|
2,29
|
2,17
|
2,02
|
1,83
|
1,61
|
1,25
|
|
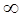
|
3,84
|
2,99
|
2,60
|
2,37
|
2,21
|
2,09
|
1,94
|
1,75
|
1,52
|
1,00
|
ПРИЛОЖЕНИЕ С
Значения F при Р = 0,01
|
|
1
|
2
|
3
|
4
|
5
|
6
|
8
|
12
|
24
|
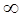
|
|
1
|
4052
|
4999
|
5403
|
5625
|
5764
|
5859
|
5981
|
6106
|
6234
|
6366
|
|
2
|
98,49
|
99,00
|
99,17
|
99,25
|
99,30
|
99,33
|
99,36
|
99,42
|
99,46
|
99,50
|
|
3
|
34,12
|
30,81
|
29,46
|
28,71
|
28,24
|
27,91
|
27,49
|
27,05
|
26,60
|
26,12
|
|
4
|
21,20
|
18,00
|
16,69
|
15,98
|
15,52
|
15,21
|
14,80
|
14,37
|
13,93
|
13,46
|
|
5
|
16,26
|
13,27
|
12,06
|
11,39
|
10,97
|
10,67
|
10,29
|
9,89
|
9,47
|
9,02
|
|
6
|
13,74
|
10,92
|
9,78
|
9,15
|
8,75
|
8,47
|
8,10
|
7,72
|
7,31
|
6,88
|
|
7
|
12,25
|
9,55
|
8,45
|
7,85
|
7,46
|
7,19
|
6,84
|
6,47
|
6,06
|
5,65
|
|
8
|
11,26
|
8,65
|
7,59
|
7,01
|
6,63
|
6,37
|
6,03
|
5,67
|
5,28
|
4,86
|
|
9
|
10,56
|
8,02
|
6,99
|
6,42
|
6,06
|
5,80
|
5,47
|
5,11
|
4,73
|
4,31
|
|
10
|
10,04
|
7,56
|
6,55
|
5,99
|
5,64
|
5,39
|
5,06
|
4,71
|
4,33
|
3,91
|
|
11
|
9,65
|
7,20
|
6,22
|
5,67
|
5,32
|
5,07
|
4,74
|
4,40
|
4,02
|
3,60
|
|
12
|
9,33
|
6,93
|
5,95
|
5,41
|
5,06
|
4,82
|
4,50
|
4,16
|
3,78
|
3,36
|
|
13
|
9,07
|
6,70
|
5,74
|
5,20
|
4,86
|
4,62
|
4,30
|
3,96
|
3,59
|
3,16
|
|
14
|
8,86
|
6,51
|
5,56
|
5,03
|
4,69
|
4,46
|
4,14
|
3,80
|
3,43
|
3,00
|
|
15
|
8,68
|
6,36
|
5,42
|
4,89
|
4,56
|
4,32
|
4,00
|
3,67
|
3,29
|
2,87
|
|
16
|
8,53
|
6,23
|
5,29
|
4,77
|
4,44
|
4,20
|
3,89
|
3,55
|
3,18
|
2,75
|
|
17
|
8,40
|
6,11
|
5,18
|
4,67
|
4,34
|
4,10
|
3,79
|
3,45
|
3,08
|
2,65
|
|
18
|
8,28
|
6,01
|
5,09
|
4,58
|
4,25
|
4,01
|
3,71
|
3,37
|
3,00
|
2,57
|
|
19
|
8,18
|
5,93
|
5,01
|
4,50
|
4,17
|
3,94
|
3,63
|
3,30
|
2,92
|
2,49
|
|
20
|
8,10
|
5,85
|
4,94
|
4,43
|
4,10
|
3,87
|
3,56
|
3,23
|
2,86
|
2,42
|
|
21
|
8,02
|
5,78
|
4,87
|
4,37
|
4,04
|
3,81
|
3,51
|
3.17
|
2,80
|
2,36
|
|
22
|
7,94
|
5,72
|
4,82
|
4,31
|
3,99
|
3,76
|
3,45
|
3,12
|
2,75
|
2,31
|
|
23
|
7,88
|
5,66
|
4,76
|
4,26
|
3,94
|
3,71
|
3,41
|
3,07
|
2,70
|
2,26
|
|
24
|
7,82
|
5,61
|
4,72
|
4,22
|
3,90
|
3,67
|
3,36
|
3,03
|
2,66
|
2,21
|
|
25
|
7,77
|
5,57
|
4,68
|
4,18
|
3,86
|
3,63
|
3,32
|
2,99
|
2,62
|
2,17
|
|
26
|
7,72
|
5,53
|
4,64
|
4,14
|
3,82
|
3,59
|
3,29
|
2,96
|
2,58
|
2,13
|
|
27
|
7,68
|
5,49
|
4,60
|
4,11
|
3,78
|
3,56
|
3,26
|
2,93
|
2,55
|
2,10
|
|
28
|
7,64
|
5,45
|
4,57
|
4,07
|
3,75
|
3,53
|
3,23
|
2,90
|
2,52
|
2,06
|
|
29
|
7,60
|
5,42
|
4,54
|
4,04
|
3,73
|
3,50
|
3,20
|
2,87
|
2,49
|
2.03
|
|
30
|
7,56
|
5,39
|
4,51
|
4,02
|
3,70
|
3,47
|
3,17
|
2,84
|
2,47
|
2,01
|
|
40
|
7,31
|
5,18
|
4.31
|
3,83
|
3,51
|
3,29
|
2,99
|
2,66
|
2,29
|
1,80
|
|
60
|
7,08
|
4,98
|
4.13
|
3,65
|
3,34
|
3,12
|
2,82
|
2,50
|
2,12
|
1,60
|
|
120
|
6,85
|
4,79
|
3,95
|
3,48
|
3,17
|
2,96
|
2,66
|
2,34
|
1,95
|
1,38
|
|
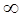
|
6,64
|
4,60
|
3,78
|
3,32
|
3,02
|
2,80
|
2,52
|
2,18
|
1,79
|
1,00
|
План 2003
Составитель
Юрий Григорьевич
Сильвестров
ОЦЕНКА ДИСПЕРСИИ
В ЗАДАЧАХ
СТАТИСТИЧЕСКОГО
КОНТРОЛЯ КАЧЕСТВА
Методические
рекомендации
к выполнению
практической работы по курсу
«Статистические методы
управления качеством»
для студентов специальности
«Управление качеством» (340100)
Напечатано в полном соответствии с авторским
оригиналом
Изд. лиц. № 1439
от 08.04.2000 г. Подписано в печать
Формат бумаги
60х84 1/16. Бумага писчая. Ризография.
Усл. печ. л. .
Уч.-изд. л. . Тираж 50 экз. Заказ .
ГОУ ВПО
«Сибирский государственный индустриальный университет»
654007, г.
Новокузнецк, ул. Кирова 42.
Издательский
центр ГОУ ВПО СибГИУ
|