Министерство
образования Российской федерации
Государственное образовательное учреждение
высшего
профессионального образования
«Сибирский государственный индустриальный
университет»
Кафедра металлургии и технологии
сварочного производства
ПРАКТИЧЕСКОЕ
ПРИМЕНЕНИЕ
БИНОМИАЛЬНОГО
РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ СОБЫТИЙ
В ЗАДАЧАХ
СТАТИСТИЧЕСКОГО КОНТРОЛЯ
Методические
рекомендации
к выполнению
практической работы по курсу
«Статистические методы
управления качеством»
для студентов
специальности «Управление качеством» (340100)
Новокузнецк
2003
УДК 658.56
Рецензент
Кандидат технических наук, доцент кафедры
электрометаллургии, стандартизации и сертификации ГОУ ВПО «СибГИУ»
Практическое применение биномиального
распределения случайных событий в задачах статистического контроля. Метод.
рек. /Сост.: Ю.Г. Сильвестров: ГОУ ВПО «СибГИУ». - Новокузнецк, 2003, - 13 с.
Изложены
общие теоретические положения применения биномиального распределения при
выборочном контроле параметров качества, характеризуемых альтернативными
признаками. Даны задачи для самостоятельного решения и закрепления
материала.
Предназначены
для студентов специальности «Управление качеством» (340100)
по курсу «Статистические методы управления качеством».
1. ЦЕЛЬ РАБОТЫ
1.1.
Ознакомиться с законом биномиального распределения, его числовыми
характеристиками и способами подсчета вероятностей.
1.2.
Закрепить полученные знания при решении практических задач.
2. ОБЩИЕ
ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
При статистическом контроле
качества часто встречаются задачи, когда продукция оценивается
альтернативным (качественным) признаком. В таких случаях результат каждого
отдельного наблюдения основан на констатации факта: произошло или нет
определенное событие. Таким событием, может быть, например, установление
факта, что рассматриваемое изделие является бракованным, или второго сорта,
или требует доработки.
Для того, чтобы сделать вывод о
пригодности изделия и о том ”хорошее” оно или “плохое” могут быть
использованы предельные калибры или эталоны, либо визуальный контроль, либо
другие методы неколичественной оценки. При применении предельных калибров
сознательно отказываются от измерений, дающих численные значения признака.
В альтернативу хорошо – плохо
можно превратить и распределение количественного признака продукции,
используя, например, трехсигмовые границы. Если наблюдаемый признак лежит
внутри этих границ: 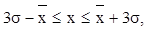 то
изделие считается годным, если вне их - то бракованным. то
изделие считается годным, если вне их - то бракованным.
При выборочном контроле
качественных признаков, в зависимости от характера случайных событий и
объема выборки, чаще всего используют либо биномиальное распределение, либо
распределение Пуассона.
Биномиальное распределение
используют обычно в том случае, если объем
выборки n не очень велик, а вероятность
случайного события p,
или ему противоположного - q, не очень малы.
Можно так сформулировать закон
биномиального распределения в применении к контролю качества. Если
вероятность появления брака постоянна при производстве серии изделий
(генеральной совокупности) и равна p, то вероятность появления
брака x раз в выборке размером n изделий будет равна:
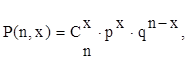 (1)
(1)
где q – вероятность непоявления брака, равная 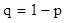 . .
В выражении (1) коэффициент 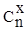 есть число
сочетаний из n по x, т.е. число способов, которыми
можно выбрать x
бракованных
изделий из совокупности n
изделий. есть число
сочетаний из n по x, т.е. число способов, которыми
можно выбрать x
бракованных
изделий из совокупности n
изделий.
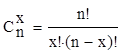 (2) (2)
Для того, чтобы построить ряд
распределения, необходимо по формуле (1) определить вероятность 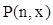 для всех x,
начиная с x=0 и заканчивая x=n. для всех x,
начиная с x=0 и заканчивая x=n.
Числовые характеристики
биномиального ряда распределения имеют следующие значения:
математическое ожидание: 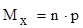 , (3) , (3)
дисперсия: 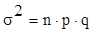 ,
(4) ,
(4)
стандартное отклонение: 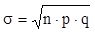 , (5) , (5)
2. СПОСОБЫ
ПОДСЧЕТА ВЕРОЯТНОСТЕЙ 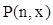
В практике
статистических расчетов используют несколько способов подсчета вероятностей
случайных величин, распределенных по биноминальному закону.
1.
При небольшой величине выборки n
используют формулы (1) и(2), определяя биноминальные коэффициенты 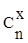 прямым расчетом
с помощью калькулятора. прямым расчетом
с помощью калькулятора.
2.
Второй способ предполагает использование таблицы кумулятивных
биноминальных вероятностей (Приложение). Такая таблица определяет
вероятность получения 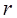 или
более бракованных деталей в выборке из n деталей. или
более бракованных деталей в выборке из n деталей.
При подсчете кумулятивных вероятностей используется следующая
формула:
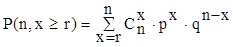 .
(6) .
(6)
Пусть, например, 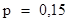 , , 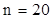 , , 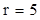 . Найти . Найти 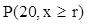 . В таблице из приложения находим столбец для вероятности . В таблице из приложения находим столбец для вероятности
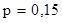 .
Найдя блок для .
Найдя блок для 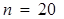 на
пересечении строки для на
пересечении строки для 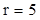 и
столбца для и
столбца для 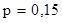 находим
искомое число: находим
искомое число:
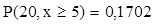
Таблица кумулятивных вероятностей может быть также использована
для вычисления вероятностей следующих событий:
получение менее 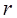 бракованных
изделий и получение ровно бракованных
изделий и получение ровно 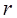 бракованных
изделий. бракованных
изделий.
Для
определения вероятности получения в выборке менее 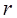 бракованных бракованных |