|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
8
|
12
|
24
|
|
|
1
|
4052
|
4999
|
5403
|
5625
|
5764
|
5859
|
5981
|
6106
|
6234
|
6366
|
|
2
|
98,49
|
99,00
|
99,17
|
99,25
|
99,30
|
99,33
|
99,36
|
99,42
|
99,46
|
99,50
|
|
3
|
34,12
|
30,81
|
29,46
|
28,71
|
28,24
|
27,91
|
27,49
|
27,05
|
26,60
|
26,12
|
|
4
|
21,20
|
18,00
|
16,69
|
15,98
|
15,52
|
15,21
|
14,80
|
14,37
|
13,93
|
13,46
|
|
5
|
16,26
|
13,27
|
12,06
|
11,39
|
10,97
|
10,67
|
10,29
|
9,89
|
9,47
|
9,02
|
|
6
|
13,74
|
10,92
|
9,78
|
9,15
|
8,75
|
8,47
|
8,10
|
7,72
|
7,31
|
6,88
|
|
7
|
12,25
|
9,55
|
8,45
|
7,85
|
7,46
|
7,19
|
6,84
|
6,47
|
6,06
|
5,65
|
|
8
|
11,26
|
8,65
|
7,59
|
7,01
|
6,63
|
6,37
|
6,03
|
5,67
|
5,28
|
4,86
|
|
9
|
10,56
|
8,02
|
6,99
|
6,42
|
6,06
|
5,80
|
5,47
|
5,11
|
4,73
|
4,31
|
|
10
|
10,04
|
7,56
|
6,55
|
5,99
|
5,64
|
5,39
|
5,06
|
4,71
|
4,33
|
3,91
|
|
11
|
9,65
|
7,20
|
6,22
|
5,67
|
5,32
|
5,07
|
4,74
|
4,40
|
4,02
|
3,60
|
|
12
|
9,33
|
6,93
|
5,95
|
5,41
|
5,06
|
4,82
|
4,50
|
4,16
|
3,78
|
3,36
|
|
13
|
9,07
|
6,70
|
5,74
|
5,20
|
4,86
|
4,62
|
4,30
|
3,96
|
3,59
|
3,16
|
|
14
|
8,86
|
6,51
|
5,56
|
5,03
|
4,69
|
4,46
|
4,14
|
3,80
|
3,43
|
3,00
|
|
15
|
8,68
|
6,36
|
5,42
|
4,89
|
4,56
|
4,32
|
4,00
|
3,67
|
3,29
|
2,87
|
|
16
|
8,53
|
6,23
|
5,29
|
4,77
|
4,44
|
4,20
|
3,89
|
3,55
|
3,18
|
2,75
|
|
17
|
8,40
|
6,11
|
5,18
|
4,67
|
4,34
|
4,10
|
3,79
|
3,45
|
3,08
|
2,65
|
|
18
|
8,28
|
6,01
|
5,09
|
4,58
|
4,25
|
4,01
|
3,71
|
3,37
|
3,00
|
2,57
|
|
19
|
8,18
|
5,93
|
5,01
|
4,50
|
4,17
|
3,94
|
3,63
|
3,30
|
2,92
|
2,49
|
|
20
|
8,10
|
5,85
|
4,94
|
4,43
|
4,10
|
3,87
|
3,56
|
3,23
|
2,86
|
2,42
|
|
21
|
8,02
|
5,78
|
4,87
|
4,37
|
4,04
|
3,81
|
3,51
|
3.17
|
2,80
|
2,36
|
|
22
|
7,94
|
5,72
|
4,82
|
4,31
|
3,99
|
3,76
|
3,45
|
3,12
|
2,75
|
2,31
|
|
23
|
7,88
|
5,66
|
4,76
|
4,26
|
3,94
|
3,71
|
3,41
|
3,07
|
2,70
|
2,26
|
|
24
|
7,82
|
5,61
|
4,72
|
4,22
|
3,90
|
3,67
|
3,36
|
3,03
|
2,66
|
2,21
|
|
25
|
7,77
|
5,57
|
4,68
|
4,18
|
3,86
|
3,63
|
3,32
|
2,99
|
2,62
|
2,17
|
|
26
|
7,72
|
5,53
|
4,64
|
4,14
|
3,82
|
3,59
|
3,29
|
2,96
|
2,58
|
2,13
|
|
27
|
7,68
|
5,49
|
4,60
|
4,11
|
3,78
|
3,56
|
3,26
|
2,93
|
2,55
|
2,10
|
|
28
|
7,64
|
5,45
|
4,57
|
4,07
|
3,75
|
3,53
|
3,23
|
2,90
|
2,52
|
2,06
|
|
29
|
7,60
|
5,42
|
4,54
|
4,04
|
3,73
|
3,50
|
3,20
|
2,87
|
2,49
|
2.03
|
|
30
|
7,56
|
5,39
|
4,51
|
4,02
|
3,70
|
3,47
|
3,17
|
2,84
|
2,47
|
2,01
|
|
40
|
7,31
|
5,18
|
4.31
|
3,83
|
3,51
|
3,29
|
2,99
|
2,66
|
2,29
|
1,80
|
|
60
|
7,08
|
4,98
|
4.13
|
3,65
|
3,34
|
3,12
|
2,82
|
2,50
|
2,12
|
1,60
|
|
120
|
6,85
|
4,79
|
3,95
|
3,48
|
3,17
|
2,96
|
2,66
|
2,34
|
1,95
|
1,38
|
|
|
6,64
|
4,60
|
3,78
|
3,32
|
3,02
|
2,80
|
2,52
|
2,18
|
1,79
|
1,00
|
План 2003
Составитель
|
|
|
1. ЦЕЛЬ РАБОТЫ
1.1.
Ознакомиться с основными теоретическими положениями о проверки
гипотез о дисперсиях нормально распределенных генеральных совокупностей.
1.2.
Закрепить полученные знания при решении практических задач.
2. Проверка гипотезы о дисперсии нормально
распределенной генеральной совокупности.
Методы проверки дисперсии имеют особую важность
при анализе точности и стабильности технологических процессов,
измерительных приборов и станков.
Пусть на основании предшествующих опытных данных
контроля деталей, обрабатываемых на станке, известно, что величины их
диаметра имеют нормальное распределение со стандартным отклонением 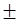 20 20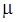 км ( км (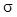 2=400 2=400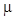 км2). км2).
С целью
проверки постоянства настройки станка берется выборка объемом n=20 и рассчитываются ее статические характеристики:
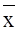 = 20 мм; S2 = 841 = 20 мм; S2 = 841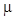 км2; S = 29 км2; S = 29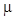 км. км.
Можно ли на основании этих
результатов заключить, что станок настроен как обычно, или величина S = 29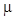 км
говорит о несоответствии станка предъявляемым требованиям. км
говорит о несоответствии станка предъявляемым требованиям.
Последовательность решения такой задачи выглядит
следующим образом. Предполагают, что выборка взята из генеральной
совокупности с 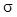 0
= 20 0
= 20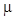 км, т.е.
проверяемая гипотеза гласит: Н0: км, т.е.
проверяемая гипотеза гласит: Н0: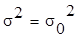 . Эту гипотезу
проверяют по выборочной характеристике . Эту гипотезу
проверяют по выборочной характеристике 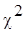 (кси –квадрат) : (кси –квадрат) :
|
|