Табулирование – это построение таблиц или статистических распределенй, в которых каждой варианте xi поставлена в соответствие её частота fi в выборке или при необходимости – частость ωі. Для того чтобы совершить табулирование, необходимо упорядочить (расположить варианты в заданной последовательности) исходный материал, а также сгруппировать (объединить варианты в интервалы) его.
Например, в эксперименте при исследовании натуральной памяти (методика А. Р. Лурия) у 30 испытуемых после первого предъявления слов были получены такие результаты: 5, 3, 5, 4, 5, 3, 1, 4, 6, 2, 5, 7, 4, 2, 5, 6, 3, 6, 5, 4, 3, 3, 4, 5, 6, 2, 3, 4, 4, 7.
Если упорядочить и сгруппировать варианты по признаку возрастания, то получим такой статистический ряд: 1, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7.
Протабулировав варианты, получаем такое статистическое распределение, которое представлено в таблице 3.2.
Таблица 3.2
Показатели частоты и частости вариант в выборке для испытуемых в исследовании натуральной памяти (методика А. Р. Лурия) после первого предъявления слов (N=30)
|
Xі |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Fі |
1 |
3 |
6 |
7 |
7 |
4 |
2 |
|
Ωі% |
3,3 |
10 |
20 |
23,3 |
23,3 |
13,3 |
6,7 |
Последующим этапом первоначальной обработки исходного материала, полученного в результате исследования, является графическое представление статистического распределения. В математической статистике существует два вида графических представлений статистического распределения: полигон частот, гистограмма.
Полигон частот – это ломаная линия, соединяющая точки, соответствующие величинам частот (ось ординат) и величинам вариант (ось абсцисс). На рис. 3.2 дан полигон частот для вышеуказанного примера (по результатам табл. 3.2) в виде жирной ломаной линии.
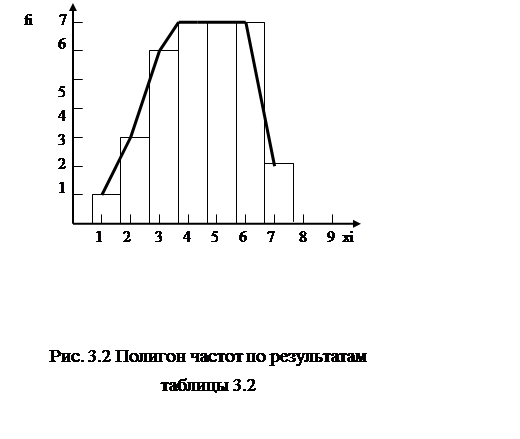 |
Гистограмма – это график в виде прямоугольников, основанием которых (ось абсцисс) является интервал вариант, а высота – частотный интервал (ось ординат). На рисунке 3.2 представлена гистограмма статистического распределения для того же самого примера в виде прямоугольников.
3. 3. Средняя арифметическая величина и её вычисление
Среднее значение – это некий обобщающий показатель положения и уровня центра расположения, т. е. того значения признака, вокруг которого концентрируется все другие варьирующие значения. В математической статистике существует множество видов средних величин, за каждой из которых кроется определённое содержание, дающее количественную и качественную оценку изучаемого признака. Данный показатель является специфической абстракцией, позволяющей опосредованно представить различные характеристики исходной выборки. Выбор средней непосредственно связан со спецификой анализа полученных данных в эксперименте.
Средняя арифметическая величина исчисляется такой формулой:
|
![]()
![]()
В данной формуле xi – значение варианты с номером от 1 доn, fi – частота соответствующей варианты, N – объём выборки.
Для вышеназванного примера имеем:
1 · 1 + 2 · 3 + 3 · 6 + 4 · 7 + 5 · 7 + 6 · 7 + 7 · 2 144
![]() ар
=
––––––––––––––––––––––––––––––––––––– = ––– = 4, 8
ар
=
––––––––––––––––––––––––––––––––––––– = ––– = 4, 8
30 30
Средняя арифметическая несёт в себе смысл суммирования всех исходных вариант и равномерного распределения общего количества измереного показателя между всеми вариантами, количество которых равно N.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.