220400 Математический анализ Толстиков А.В.
Курс 1. Семестр 2. Лекция 12. Числовые ряды
План
1. Числовые ряды. Сходимость и сумма ряда. Действия с рядами.
2. Необходимый признак сходимости. Ряд геометрической прогрессии. Гармонический ряд.
3. Ряды с неотрицательными членами. Признаки сравнений.
4. Достаточные признаки сходимости знакопостоянного ряда Даламбера, Коши, интегральный прзнак.
5. Знакочередующиеся ряды. Признак Лейбница.
6. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимости ряда.
7. Свойства абсолютно сходящихся рядов.
Литература: Архипов А.И. с.347-387. Ильин В.А., т. 1, с.411 - 442. Ермаков В.И., с.320-330. Крамер В.Ш., с.356-377.
1. Числовые ряды. Сходимость и сумма ряда. Действия с рядами..
Определение 1. Числовым рядом называется выражение вида
![]() ,
(1)
,
(1)
где {an} = {a1, a2, …, an, …} - произвольная последовательность действительных или комплексных чисел, называемых членами ряда. Число an называются общим членом ряда (1).
Определение 2.
Сумма a1 + a2, + …+ an первых n членов ряда (1) называется n -
частичной суммой ряд (1) и обозначается символом Sn: S1 = a1,
S2 = a1 + a2,
…, ![]() .
.
Определение 3.
Числовой ряд (1) называется сходящимся, если существует конечный предел
последовательности его частичных сумм, т.е. ![]() .
При этом сам предел S последовательности
его частичных сумм называется суммой ряда. В этом случае можно
записывать
.
При этом сам предел S последовательности
его частичных сумм называется суммой ряда. В этом случае можно
записывать
![]() .
(2)
.
(2)
Если предела ![]() не
существует, то ряд называется расходящимся.
не
существует, то ряд называется расходящимся.
Определение 4.
Произведением числового ряда (1) на число с называется ряд ![]() .
.
Определение 5.
Суммой (разностью) двух числовых рядов ![]() называется
соответственно ряды
называется
соответственно ряды ![]() .
.
Определение 6.
Произведением двух числовых рядов ![]() называется
числовой ряд
называется
числовой ряд ![]() .
.
Теорема 1. Если
ряд (1) сходится и имеет сумму S, то ряд ![]() , полученный
умножением данного ряда на число c, также сходится
и имеет сумму cS.
, полученный
умножением данного ряда на число c, также сходится
и имеет сумму cS.
Теорема 2. Если
ряды ![]() сходится и
имеет соответственно суммы S1,
S2 , то ряды
сходится и
имеет соответственно суммы S1,
S2 , то ряды ![]() сходятся
и имеют соответственно суммы S1 + S2 и S1 - S2.
сходятся
и имеют соответственно суммы S1 + S2 и S1 - S2.
Теорема 3. Если ряд сходится (1), то сходится и ряд, полученный из данного ряда путем отбрасывания (или добавления к ряду) конечного числа членов.
2. Признак Коши. Необходимый признак сходимости. Ряд геометрической прогрессии. Гармонический ряд.
Теорема 1(критерий сходимости Коши для ряда). Для того, что бы ряд (1) сходился необходимо и достаточно, чтобы для любого e нашелся такой номер N0 , что для всех номеров n > N0 и любых натуральных чисел p, выполняется неравенство
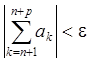 .
(3)
.
(3)
Доказательство. По определению ряд (1) сходится тогда и только тогда, когда сходится его последовательность Sn частичных сумм. По критерию Коши для последовательностей она сходится тогда и только тогда, для любого e найдется такой номер N0 , что для всех номеров n > N0 и любых натуральных чисел p, выполняется неравенство|Sn+p - Sn|< e., что для всех , удовлетворяющих условию выполняется неравенство. Так как последнее неравенство равносильно неравенству (3), то отсюда следует утверждение теоремы 1.
Ряд ![]() называется n-м остатком
ряда (1).
называется n-м остатком
ряда (1).
Теорема 2(необходимый
признак сходимости ряда). Если ряд (1) сходился, то предел общего
члена an ряда при n ®¥ равен нулю, т.е. ![]() .
.
Следствие(достаточный признак расходимости ряда). Если предел общего члена an ряда при n ®¥ не равен нулю, то ряд расходится.
Исследуем сходимость ряда
![]() ,
(4)
,
(4)
который называется рядом геометрической прогрессии.
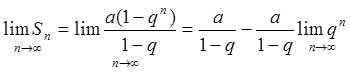 .
.
Теорема 3. Ряд (4) геометрической прогрессии сходился при |q| < 1 и расходится при |q| ³ 1.
Исследуем сходимость ряда
![]() ,
(4)
,
(4)
который называется гармоническим рядом при p = 1, обобщенным гармоническим рядом для произвольного р.
Теорема 3. Гармонический ряд расходится. Обобщенный гармонический ряд сходился при p > 1 и расходится при p £ 1.
Доказательство. Если
гармонический ряд сходится, то для любого e, в том числе
для e = 0,5 , найдется такой номер N0 , что для всех номеров n > N0 и любых натуральных чисел p,
выполняется неравенство ![]() . Возьмем и тогда получим
. Возьмем и тогда получим
![]() .
.
Это дает противоречие со сказанным выше. Теорема доказана.
3. Ряды с неотрицательными членами. Признаки сравнений. Ряд, все члены которого больше или равны нуля, называется рядом с неотрицательными членами. Если все члены ряда больше нуля, то ряд называется рядом с положительными членами.
Теорема 1. Ряд с положительными членами сходится тогда и только тогда, когда последовательность частичных сумм ряда ограничена.
Доказательство. Необходимость. Если ряд (1) сходится, то сходится его последовательность Sn частичных сумм. Тогда по теоремы об ограниченности сходящейся числовой последовательности Sn ограничена.
Достаточность.
Для ряда с положительными членами Sn+1 > Sn , последовательность Sn
его частичных сумм возрастает, и по теоремы о существовании предела монотонной
ограниченной последовательности существует предел ![]() .
Тогда ряд сходится.
.
Тогда ряд сходится.
Теорема 2 (признак
сравнений). Пусть даны два ряда ![]() с
положительными членами, при чем члены первого ряда не превосходят
соответствующих членов второго ряда . т.е. при любом n имеем
an£bn.
Тогда
с
положительными членами, при чем члены первого ряда не превосходят
соответствующих членов второго ряда . т.е. при любом n имеем
an£bn.
Тогда
1) если сходится второй ряд, то сходится и первый ряд;
2) если расходится первый ряд, то расходится и второй.
Доказательство. 1) Если ряд
(2) сходится, то существует предел последовательность Sn'' его частичных
сумм, ![]() .
По условию частичные суммы Sn'
первого ряда не превосходят частичных сумм Sn'', второго ряда,
Sn'£ S
''. Тогда последовательность
Sn' по
теоремы об ограниченной монотонной последовательности сходится и ряд (1)
сходится. Методом от противного доказывается вторая часть теоремы.
.
По условию частичные суммы Sn'
первого ряда не превосходят частичных сумм Sn'', второго ряда,
Sn'£ S
''. Тогда последовательность
Sn' по
теоремы об ограниченной монотонной последовательности сходится и ряд (1)
сходится. Методом от противного доказывается вторая часть теоремы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.