Числовые ряды. Сходимость и сумма ряда. Действия с рядами. Свойства абсолютно сходящихся рядов, страница 3

2)  предел общего члена ряда (1) равен нулю, т.е. .

Тогда ряд (1) сходится.

Доказательство. Так как , то при возрастании последовательность {S_2n} не убывает. Так как . Тогда последовательность  {S_2n} сходится, т.е. .  Так как S_2n+1 = S_2n + a_2n+1, то  . Тогда .

6.  Знакопеременные ряды, ряды с комплексными членами. Ряд, который содержит бесконечно много как положительных членов так и отрицательных членов называется знакопеременным.

Мы также рассматриваем ряды с комплексными членами

.                                                       (1)

Рассмотрение ряда с комплексными членами равносильно рассмотрению двух рядов, составленных соответственно из действительных и мнимых частей членов ряд (1).  В том числе справедлив критерий сходимости Коши. Определение сходимости ряда (1) равносильно определению сходимости из пункта (1).

Теорема 1 . Ряд с комплексными членами (1) сходится тогда и только тогда, когда сходятся ряды (2) и (3), составленные из действительных и мнимых частей ряда (1). При этом сумма ряда (1) равна S = S₁ + iS₂, где S₁, S₂ - соответственно суммы рядов (2) и (3).

Теорема 2 . Если сходится ряд

                                                                  (2)

составленный из модулей членов ряда (1), то сходится и ряд (1).

Доказательство. Следует из критерия Коши и неравенства .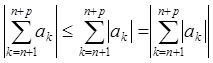

с комплексными членами (1)  сходится, еи (3), составленные из действительных и мнимых частей ряда (1). При этом сумма ряда (1) равна S = S₁ + iS₂, где S₁, S₂ - соответственно суммы рядов (2) и (3).

Следствие 2 . Если сходится ряд, составленный из модулей членов знакопеременного ряда, то сходится и сам ряд.

7.  Абсолютная и условная сходимости ряда. Свойства абсолютно сходящихся рядов.

Определение 1. Ряд с действительными или комплексными членами называется абсолютно сходящимся, если сходится ряд, составленный из модулей членов данного ряда.

Определение 2. Ряд с действительными или комплексными членами называется условно сходящимся, если сам ряд сходится, а  ряд, составленный из модулей членов данного ряда расходится.

В силу теоремы (2) предыдущего параграфа, если ряд сходится абсолютно, то он сходится и условно. Обратное неверно. Например, ряд  сходится условно, но не сходится абсолютно.

Свойства абсолютно сходящихся рядов.

Теорема 1 (теорема Дирихле). Если ряд абсолютно сходится к сумме S, то к этой же сумме S сходится ряд, полученный из данного ряда любой перестановкой членов.

Теорема 2 . Сумма, разность, произведение двух абсолютно сходящихся рядов есть абсолютно сходящиеся ряды. При этом сумма абсолютно сходящихся рядов равна  S₁+ S₂(разность абсолютно сходящихся рядов равна  S₁- S₂, произведение абсолютно сходящихся рядов равно  S₁ S₂), где S₁ , S₂ соответственно суммы первого и второго рядов.

Замечание. Члены условно сходящегося ряда нельзя переставлять, так как по теореме Римана в этом случае можно получить условно сходящийся ряд с заранее заданной суммой или расходящийся ряд.

Действия над рядами можно производить, если ряды абсолютно сходятся.