4.2.3.6. Методы первого порядка
Рассматриваемые методы базируются на использовании вектора градиента ЦФ. В связи с этим они также называются также градиентными.
Напомним, что градиентом функции n переменных z(X) называется вектор, компонентами которого являются частные производные первого порядка этой функции в точке X (см. формулу (4.8)). Антиградиентом называется вектор – gradz(X).
Вектор-градиент ЦФ z(X) обладает следующим важным свойством: направление градиента в точке X совпадает с направлением наискорейшего возрастания ЦФ в этой точке. Таким образом, направление вектора градиента задает локально наилучшее направление изменения ЦФ при ее максимизации. Соответственно, направление антиградиента задает локально наилучшее направление минимизации ЦФ.
Вектор-градиент содержит также информацию о скорости возрастания целевой функции: его отдельные компоненты определяют скорость возрастания отдельно по каждой координате, а модуль – общую скорость возрастания ЦФ.
В связи с указанными свойствами градиента естественно построение пошаговой процедуры минимизации ЦФ вида (4.9), в которой в качестве вектора направления Sk используется направление, задаваемое вектором-антиградиентом -grad z(X).
Градиентные методы можно определить, таким образом, как методы поиска, в которых направление движения от итерации Xk к итерации Xk+1 определяется градиентом (антиградиентом), вычисленным в точке Xk.
В градиентных методах помимо собственно вектора grad z(X) часто используется нормированный вектор градиента gz(X), определяемый в виде:
gz(X) = grad z(X) / | grad z(X) | , (4.21)
где | grad z(X) | - модуль (или норма) вектора grad z(X), рассчитываемый (рассчитываемая) как квадратный корень из суммы квадратов компонент этого вектора. Очевидно, что модуль вектора gz(X) равен единице.
З а м е ч а н и я 4.22. 1) Для обозначения вектора градиента наряду с символом “grad” часто используется символ “Ñ” (набла).
2) В точке экстремума целевой функции ее градиент равен нулю (см. (4.7)).
Возможны два способа вычисления значения градиента в некоторой точке: аналитический и численный.
В первом случае в результате дифференцирования ЦФ находятся соответствующие аналитические выражения компонент градиента, по которым затем для заданной точки подсчитываются численные значения компонент градиента.
Во втором случае значения каждой из частных производных приближенно представляются отношениями конечных разностей [26,54]. Так, для j-ой компоненты вектора градиента может использоваться следующее соотношение:
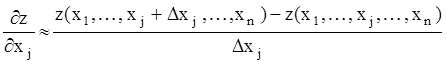(4.22)
где Dxj – величина приращения независимой переменной
З а м е ч а н и е 4.23. На практике используется и другой вид формулы (4.22) в которой j-ые аргументы вычитаемых ЦФ имеют вид xj +Dxj и xj -Dxj соответственно, а в знаменателе стоит 2Dxj.
Метод градиента.
Рассматриваемый метод имеет несколько разновидностей, отличающихся видом рекурсивных формул, описывающих процедуру построения последовательности {Xk}, минимизирующей ЦФ.
Первая разновидность предполагает использование градиента и постоянного шага [10,15,20,24,26], вторая – градиента и переменного шага [4,18,20,26], третья – нормированного вектора градиента и переменного шага [26,53,54].
Соответствующие рекурсивные формулы имеют вид:
Xk+1 = Xk – h grad z(Xk), h > 0 ; (4.23)
Xk+1 = Xk – hk grad z(Xk), hk > 0, k = 0, 1, 2, … ; (4.24)
Xk+1 = Xk – hk g z(Xk), hk > 0, k = 0, 1, 2, … . (4.25)
З а м е ч а н и е 4.23. В литературе упоминается также вариант третьей разновидности метода (описываемого формулой (4.25)), предполагающий использование шага постоянной длины h [15,21,24,54]. Существенным недостатком такого варианта является большая вероятность возникновения “рыскания” в районе оптимума. В связи с этим такой вариант на практике обычно не используется.
Рассмотрим этапы построения последовательности {Xk}, описываемой формулой (4.23). Сначала задается начальная точка X0. Затем в ней производится расчет компонент вектора градиента, а затем антиградиента, который и задает направление спуска. В этом направлении осуществляется шаг длиной h, в результате чего определяется точка X1 .
В точке X1 вычисляются значения компонент вектора gradz(X1), после чего в задаваемом им направлении делается шаг той же длины h т.д.
Приведем покоординатную запись рекуррентной формулы (4.23):
 |
x k+1 j = x k j - h ¶z(Xk)/¶xj , j =1,n , k=0,1,2,… (4.26)
Подчеркнем, что характерной особенностью градиентного метода является расчет вектора - градиента в конце каждого выполненного шага.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.