Методы первого порядка. Задачи и методы условной оптимизации нелинейного программирования, страница 5

S ^k+1  =  - grad z(X ^k) + b^k S ^k-1    ,  k=1,2,3,…                                  (4.31)

где b^k – весовой коэффициент, который выбирается так, чтобы сделать S^k+1 и  S^k  сопряженными по отношению к матрице G ; S⁰ = - grad z(X⁰) .

Значение весового коэффициента  рассчитывается по следующей приближенной формуле:

b^k =  <grad z(X^k) , grad z(X^k) > / <grad z(X^k-1) , grad z(X^k-1)>       k=1,2,…    (4.32 )

Рассмотрим пошаговую процедуру построения последовательности точек {X^k } .

Первый шаг из точки X⁰ в точку X¹ осуществляется методом наискорейшего спуска:

X¹  =   X⁰  -  h⁰ grad z(X⁰)   , где h⁰ - оптимальный шаг.

Последующие шаги подсчитываются по следующей  рекуррентной формуле

X ^k+1  =  X^k   +  h^k S^k  ,       k= 0,1,2,… ,                              (4.33)

где S^k  определяется по формуле (4.31) , а оптимальная длина шага h^k - в результате решения соответствующей одномерной задачи оптимизации по направлению S^k .

Метод сопряженных градиентов применим не только для оптимизации квадратичной функции, но и функций общего вида. В последнем случае для нахождения экстремума необходимо выполнить более n шагов и осуществлять итерационный процесс. Характерная особенность такого процесса состоит в том, что после выполнения первых n шагов, сопровождающихся нахождением n сопряженных векторов, последняя найденная точка должна быть снова принята в качестве начальной и процедура нахождения сопряженных векторов должна быть повторена. Такие повторения должны осуществляться до тех пор, пока не будет выполнен критерий окончания итераций, в качестве которого обычно принимается величина градиента (см. соотношение (4.28)). Более подробно алгоритм метода рассмотрен в [35,21,18, 49].

Метод имеет улучшенные характеристики при прохождении оврагов. В [22]  рассматриваемый  метод охарактеризован как один из эффективных методов оптимизации в автоматизированном проектировании.

Метод Дэвидона-Флетчера-Пауэлла (ДФП)

Рассматриваемый метод является разновидностью группы методов, называемых методами переменной метрики [18]  или квазиньютоновскими  методами [49]. Такие методы     также можно рассматривать как попытку объединения достоинств методов первого и второго порядка. Они основаны на приближенной аппроксимации обратной матрицы Гессе.

Упомянутые методы являются  итерационными методами, в которых поиск ведется по формуле:              

X^k+1  =  X^k - h^k H ^kgrad z(X^k)   ,      k = 0,1,2,…                               (4.34 )

В этой формуле в качестве матрицы H^k используется приближенно вычисляемая обратная матрица Гессе G^-1 ; h^k – величина шага, определяемая одномерной оптимизацией ЦФ на луче  - H ^kgrad z(X^k).

Добавим, что H^k – положительно определенная симметрическая матрица, которая обновляется на каждом шаге и в пределе становится равной G^-1. Способ построения такой матрицы и определяет особенности того или иного метода

В методе Дэвидона-Флетчера-Пауэлла при поиске из начальной точки в качестве начальной матрицы принимают единичную матрицу. Первый шаг производится по методу наискорейшего спуска. Матрица H ^k вычисляется по формуле

H ^k = H ^k-1 + A(X^k-1) – B(X^k-1)                                                   (4.35)

где  A(X^k-1)= (DX^{k-1))( (DX^{k-1))^T / ((DX^{k-1))^T (Dg(X^(k-1))  ;

 ;

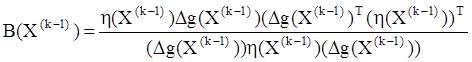Dg(X^(k-1)) = grad z(X^k) – grad z(X^(k-1)) – разность векторов-градиентов, имеет форму  вектора-строки;

DX^{k-1) = h^k-1 H ^k-1grad z(X^k-1) – приращение вектора переменных оптимизации на предыдущем (k-1)-м шаге, имеет форму вектора-столбца;

(DX^{k-1))^T – транспонированный вектор DX^{k-1) , имеющий форму вектора-строки.

Алгоритм процедуры приведен в [35, 49].

Метод обладает улучшенными характеристиками при прохождении оврагов.

В [21] отмечено, что метод ДФП – один из самых эффективных методов решения задач параметрической оптимизации. В [35] он охарактеризован как мощная оптимизационная процедура, очень эффективная при оптимизации большинства функций.