Составляем функцию Лагранжа:
L(x1, x2 , l1, l2) = 5(x1-3)2 + 10(x2 – 4)2 +l1(x1+ x2 - 8) + l2(-x1 –3x2 + 15).
Строим систему вида (4.49):
x1 [10(x1 – 3) + l1 - l2 ] = 0 ; l1 [x1 + x2 - 8] = 0 ;
x2 [20(x2 – 4) + l1 - 3l2 ] = 0 ; l2 [ -x1 - 3x2 + 15] = 0.
При решении этой системы четырех уравнений с четырьмя неизвестными необходимо рассмотреть три варианта значений неизвестных: x1>0, x2 >0; x1>0, x2 =0; x1=0, x2 >0. Для каждого из них необходимо найти решение системы. Такое решение можно осуществить, выражая из первого уравнения x1, из второго – x2 и подставляя их в третье и четвертое уравнения. Так, при рассмотрении первого из вариантов получены два решения системы: l1=0, l2=0, x1=3, x2=4 и l1= -27,5, l2= -12,5, x1=4,5, x2=3,5. Поскольку вектор L = (l1 ,l2) должен быть неотрицательным, второе решение из рассмотрения исключается. Далее проверяем, являются ли точка (X,L)=(3,4,0,0) седловой для функции L(x1, x2, l1, l2). Подставляя в функцию Лагранжа найденные l1=l2 =0, получаем функцию двух переменных L(x1, x2, 0, 0)= 5(x1 –3)2 +10(x2 –4)2 , которая при x1=3, x4=4 достигает минимума. Подставляя в ту же функцию значения x1=3, x2 = 4 получаем функцию двух переменных L(3, 4, l1, l2) = - l1 , которая при l1=0 достигает максимума. Следовательно, точка (3,4,0,0) является седловой, а решение x1= 3, x2 = 4 – оптимальным со значением оптимума z(X) = z(3,4) = 0.
Поскольку ЦФ z(X) в найденной точке оптимума выпукла, то точка минимума является единственной и нет необходимости рассматривать другие решения системы уравнений.
Рассмотренный пример показывает, что решение даже относительно простых задач НП методом, основанном на использовании условий Куна-Таккера, оказывается весьма громоздким. В общем случае решение системы вида (4.49) может быть связано с большими вычислительными трудностями, в связи с чем возникает вопрос об использовании прямых (численных) методов минимизации (не предусматривающих выполнение операций дифференцирования и решения систем уравнений).
З а м е ч а н и е 4.31. В [8,16,19] рассмотрены методы решения задач НП с ограничениями типа неравенств, сводящиеся к решению задач НП с отброшенными ограничениями или задач с ограничениями типа равенств. Однако такие методы менее удобны, чем рассмотренный выше.
З а м е ч а н и е 4.32. Использование теоремы Куна-Таккера эффективно при решении задач квадратичного программирования. С ее помощью такие задачи сводятся к задачам ЛП [5…8,16].
4.3.3.3. Численные методы решения задач оптимизации при ограничениях типа неравенств
Численные методы решения задачи НП с ограничениями типа неравенств разбиваются на три группы:
1) методы штрафных функций;
2) методы, учитывающие ограничения в явной форме;
3) методы случайного поиска
Первую группу представляют методы штрафных функций. Эти методы применительно к ограничениям-неравенствам сохраняют общую идею, изложенную в п. 4.3.2.2 (“наложение штрафа” за “выход” в область невыполнения ограничений), но имеют свои особенности.
Так, при решении задачи оптимизации (4.47) следует выбирать штрафную функцию H(x) так, чтобы она в идеале обладала следующими свойствами [4]:
H(X) =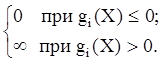 
(4.50)
Такая штрафная функция носит название “бесконечный барьер” [20] (см. рис. 4.19.а).
А б с
Рис. 4.19
Тогда точка X, минимизирующая R(X), минимизирует и z(X). Однако из-за невозможности точного представления в ЭВМ бесконечно большой величины используются различные приближенные способы задания штрафной функции вида (4.50).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.