Математика \ Методы оптимизации

Методы первого порядка. Задачи и методы условной оптимизации нелинейного программирования, страница 10

gi(X) £ 0,      i = 1, …, m,                                                     (4.47)

X ³ 0  .

Условия Куна – Таккерамогут быть представлены в различных формах. Наиболее удобная из них использует эквивалентность задачи выпуклого программирования (4.47) задаче отыскания седловой точки функции Лагранжа, построенной для этой задачи [  ]. Поясним понятие седловой точки.

Пусть для задачи (4.47) составлена функция Лагранжа (4.40). Точка (X0, L0) называется седловой точкой   функции L(X, L), если при любых X ³ 0, L³ 0 имеют место неравенства

L(X0, L) £ L(X0, L0) £ L(X, L0).                                                      (4.48)

Из неравенств (4.48) видно, что седловой является такая точка (X0, L0), в которой функция L(X, L) по направлениям (переменным) X имеет минимум, а по переменным L – максимум. Возможный вид функции L(x,l) c седловой точкой приведен на рис. 4.17.

                                          L(x,l)

 


                                                                                       x

 


                         l

Рис. 4.17.

Запишем условия существования седловой точки (x0, y0) функции Лагранжа в предположении дифференцируемости функций z(x), gi(x), а следовательно, и функции L(x,l). При отсутствии ограничений на знак переменных xj, li производные ¶L/¶xj, ¶L/¶yi в этой точке должны обратиться в нуль. При наличии ограничений xj ³ 0, li ³ 0 точка экстремума может быть на границе xj = 0 или li = 0 (рис. 4.18). Здесь, как и прежде, возможен                             

а      L(xj)                                                              б     L(li)

 


                         2                                                                                 1

 


                           1                                                                          2  

 


xj=0                                                                      li=0

Рис. 4. 18

случай равенства нулю производных по xj, yi (кривые 1, рис. 4.18, а, б). Кроме того, поскольку точка (X0, L0) есть точка минимума функции L(X, L) по переменным X и максимума по переменным L, на границе возможны значения производных ¶L(X0, L0)/¶xj > 0 и ¶L(X0,L0)/¶li <0 (кривые 2, рис. 4.18, а, б). Отсюда условия, состоящие в том, что в точке (X0,L0) всегда либо производные, либо переменные обращаются в нуль, примут вид

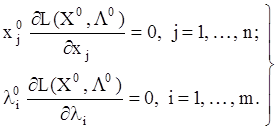                                          (4.49)

Условия (4.49) являются необходимыми условиями того, что точка (X0, L0) функции Лагранжа для задачи (4.47) является седловой точкой, и называются условиями Куна – Таккера. Понятие седловой точки используется в следующей теореме Куна-Таккера, устанавливающей признак оптимальности для задачи выпуклого программирования.

Теорема 4.1.  Для оптимальности вектора X0 в задаче (4.47) достаточно, чтобы при некотором векторе L0точка (X0, L0) была седловой для функции Лагранжа (4.40).

Доказательство такой теоремы приведено в [4]. Кроме того, Кун и Таккер дали доказательство того, что приведенный признак оптимальности является не только достаточным, но и необходимым.

Таким образом, задача выпуклого программирования (4.47) эквивалентна задаче о  седловой точке соответствующей функции Лагранжа и сводится к решению системы (4.49)  (с учетом неотрицательности компонент X и L).

Рассмотрим пример решения задачи выпуклого программирования.

Пример 4.1.  Решить задачу

min z = 5(x1 –3)2  + 10(x2 –4)2 ;

x1 + x2  £ 8 ;  x1 + 3x2 ³ 15 ;

x1 , x2  ³ 0

Скачать файл