Линейное программирование. Геометрическая интерпретация и графический метод решения задачи линейного программирования, страница 7

Поясним происхождение определения “базисный”. Переменные x₁, x₂, …, x_m носят название базисных потому, что они соответствуют некоторому базису – совокупности m линейно независимых векторов, по которым разлагается вектор свободных членов (вектор коэффициентов ограничений) системы уравнений:

A₁x₁ + A₂x₂ +…+ A_mx_m = B .

В этом разложении в качестве векторов базиса выступает часть векторов-столбцов матрицы системы, а базисные переменные являются коэффициентами разложения вектора B  по этому базису. (Упомянутое соответствие базису состоит в равенстве номера переменной номеру столбца системы уравнений  AX=B ).

Замечание 2.14. В примере 2.1 вектор B был разложен по базису A₁ , A₂ , A₃  в виде

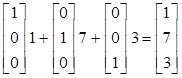
Рассмотренный выше путь решения системы уравнений с n > m не позволяет в большинстве случаев непосредственно решить задачу ЛП. Для этого необходимо предварительное преобразование исходной задачи ЛП в канонической форме  в каноническую базисную форму вида

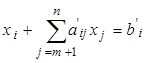,         i=1,…,m                    (2.12)

(Такая форма совпадает с приводимой ранее формой (2.5)).

Коэффициенты a¢_ij  и  b¢_i  в  (2.12)  определяются путем специальных эквивалентных преобразований коэффициентов a_ij  и  b_i формы (2.4).  (Такие преобразования  были выполнены, в частности, при получении второй системы в примере 2.1 [4].)

Базисными переменными системы (2.12) являются переменные x₁, x₂, …, x_m. Нетрудно заметить, что векторы-столбцы, соответствующие этим переменным, составляют единичный базис системы (2.12):

                         A₁ =  ,   A₂ = ,   …  ,   A_m = .

По такому базису разлагается как вектор B, так и остальные столбцы матрицы A. 

Рассматриваемые базисные векторы образуют единичную подматрицу  матрицы условий A. Наличие такой подматрицы позволяет просто найти решение системы, а именно, базисные переменные   будут определяться на основе (2.12) из соотношений:

,         i=1,…,m  , а базисное решение системы уравнений будет иметь вид

  x₁= b¢₁ ,   x₂ =b¢₂  , …,  x_m = b¢_m  , x_m+1= 0 , …, x_n = 0 .            (2.13)

Отметим, что структура базисного решения совпадает со структурой введенного ранее опорного плана. Действительно, в случае неотрицательности коэффициентов ограничений (т.е. выполнение условий b_i  ³ 0) полученное таким образом базисное решение будет также являться и опорным (а также, естественно, и допустимым). Отметим наличие связей между рассмотренным базисным решением и введенными ранее понятиями, характеризующими решения задачи ЛП. Эти связи иллюстрируются на  рисунке 2.3.

Допустимое базисное решение (сис- темы уравнений)

          

 

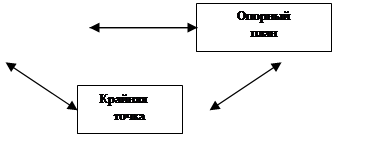Рис. 2.3 

2.5.2.   Метод исключения Жордана-Гаусса.

Рассмотрим далее так называемый метод исключений Жордана-Гаусса. В рамках вопросов, связанных с симплекс-методом, он играет двоякую роль.

Во-первых, он позволяет преобразовать систему уравнений AX=B  общего вида (2.9) в систему уравнений в базисной форме вида (2.12), допускающую простое получение базисного решения системы. (Именно в результате трехкратного применения такого эквивалентного преобразования была получена вторая система в примере 2.1 [4]). 

Во-вторых, он является одним из этапов симплекс-метода.

Метод исключений Жордана-Гаусса позволяет решить систему преобразованием ее к эквивалентной системе с единичным базисом или установить ее несовместность. В процессе преобразований при необходимости может быть построена также обратная матрица.

На каждом шаге исключений одна из переменных становится базисной: исключается из всех уравнений, кроме одного, где остается с коэффициентом 1.