Линейное программирование. Геометрическая интерпретация и графический метод решения задачи линейного программирования, страница 2

Очевидно, что стандартная и каноническая задачи являются частными случаями общей. Каждая из них используется в своей определенной области. Так, формализация производственных и планово-экономических задач приводит чаще всего к построению стандартной или общей задачи. Основные же методы решения задачи ЛП разработаны для канонической задачи.

Общая задача может быть приведена к стандартной или канонической, а последние могут быть преобразованы друг в друга так, что решение одной задачи однозначно определяет решение другой.

Опишем способы таких эквивалентных преобразований.

Для перехода от стандартной задачи с числом неравенств m и неизвестных n к канонической вводятся дополнительные неотрицательные переменные x_n+i (i = 1, …, m). При этом каждое ограничение-неравенство вида a_ijx_j £ b_i заменяется ограничением-равенством вида a_ijx_j+x_n+i  = b_i.   Дополнительные переменные включаются в ЦФ с нулевыми коэффициентами. Полученная таким образом из исходной задачи каноническая задача носит название расширенной.

Для перехода от канонической к стандартной задаче нужно каждое уравнение  a_ijx_j = b_i  заменить двумя неравенствами:

a_ijx_j  £ b_i          и      a_ijx_j ³ b_i .

Если некоторая переменная x_j не имеет ограничения на знак, то ее заменяют разностью двух переменных, например x_j = u_j-v_j, наложив условия u_j ³ 0, v_j ³ 0.

В результате этих преобразований стандартная и общая задача могут быть приведены к канонической. Таким образом, чтобы уметь решать все задачи линейного программирования, достаточно владеть способом  решения только одной из них – канонической.

2.3.  Геометрическая интерпретация и графический метод решения задачи линейного программирования

Прежде всего, отметим, что геометрическая интерпретация задачи ЛП может быть осуществлена только для стандартнойзадачи вида (2.1).

Напомним, что совокупность чисел x₁, x₂, …, x_n , удовлетво-ряющая функциональным и непосредственным ограничениям задачи МП, называется допустимым планом(решением) задачи. В задаче ЛП  в стандартной постановке такая совокупность чисел должна удовлетворять системе неравенств и условиям неотрицательности. Если задача ЛП имеет хотя бы одно допустимое решение, то она называется совместной, в противном случае несовместной.

Рассмотрим задачу ЛП в двумерном пространстве (n=2). Постановка такой задачи имеет вид:

z= c₁x₁+c₂x₂  ® max_.

при ограничениях 

                        a_i1x₁ + a_i2x₂  £ b_i , i =1, …, m ;(2.6)

x₁ ³ 0, x₂ ³ 0 .

Рассмотрим вопрос построения области допустимых решений для этой задачи.

Как известно, каждая прямая a_i1x₁+a_i2x₂ = b_i  делит плоскость на две полуплоскости. Точки (x₁, x₂) плоскости, удовлетворяющие неравенству a_i1x₁+a_i2x₂ £ b_i , находятся по одну сторону от граничной прямой и на ней, а точки, удовлетворяющие неравенству a_i1x₁+a_i2x₂ ³ b_i - по другую сторону и на самой прямой. Следовательно, для построения допустимой области, заданной неравенствами (2.6), необходимо, прежде всего, построить на плоскости многоугольник, ограниченный координатными осями x₁=0, x₂=0 и прямыми

a_i1x₁ + a_i2x₂ £ b_i  .

Так, например, для системы ограничений

x₁ + 4x₂   £ 14

3x₁ + 4x₂  £ 18                                              (2.7)

6x₁ + 2x₂   £ 27

x₁ ³ 0, x₂ ³ 0

многоугольник будет иметь вид, изображенный на рисунке 2.1.

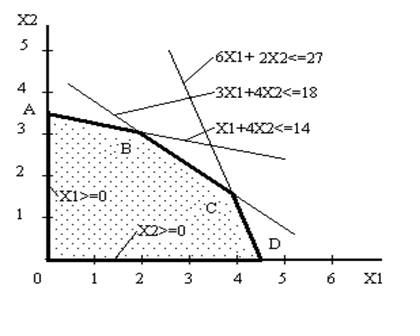Рис. 2.1

В трехмерном пространстве (n=3) каждое неравенство системы ограничений геометрически представляет собой полупространство, граничная плоскость которого

a_i1x₁+a_i2x₂+a_i3x₃=b_{i  ,}          (i=1, …, m),

а условия неотрицательности – полупространства с граничными плоскостями x_j=0 (j=1,2,3). Если система ограничений совместна, то эти полупространства, пересекаясь, образуют в трехмерном пространстве многогранник решений.

Если в системе ограничений n > 3, то каждое неравенство представляет полупространство n-мерного пространства с граничными гиперплоскостями