Линейное программирование. Геометрическая интерпретация и графический метод решения задачи линейного программирования, страница 4

В рассматриваемом примере перемещение прямой  следует осуществлять до точки C. Координаты этой крайней точки многогранника будут оптимальным решением задачи X_опт=(x₁^опт, x₂^опт). (Указанные координаты могут быть найдены также из решения системы уравнений, составленной из уравнений пересекающихся прямых.) В данной задаче X_опт= (4; 1,5). Значение максимума ЦФ  z_опт =5,5.

Таким образом, процедура графического метода решения задачи содержит два этапа: 1) построение ОДР, 2) перемещение линии равного уровня ЦФ до пересечения с крайней точкой многогранника решений.

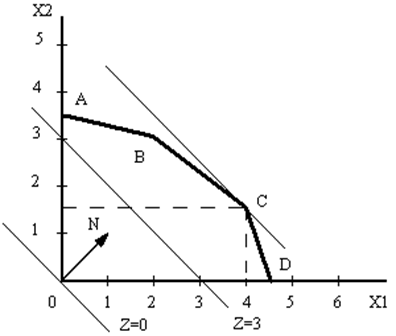Рис.  2.2.

Отметим, что в частном случае, когда коэффициенты целевой функции пропорциональны коэффициентам какого-либо ограничения, имеется множество оптимальных точек, составляющих сторону многоугольника. (Так, например, если бы целевая функция задачи имела вид z = x₁ + 4x₂, то множество оптимальных решений составляли бы все точки стороны AB).

Геометрическая интерпретация решения задачи ЛП позволяет   наглядно представить следующие возможные варианты решения  задачи вида (2.1): 1) задача имеет единственное решение, лежащее в крайней точке – вершине выпуклого многоугольника (для ограниченной или неограниченной области); 2) задача имеет бесконечное число решений, среди которых имеется хотя бы одно решение, лежащее в крайней точке допустимого многоугольника (для ограниченной или неограниченной области); 3) задача имеет допустимые решения, но не имеет оптимального решения (случай неограниченности ОДР); 4) задача не имеет допустимых решений (ограничения несовместны) а, следовательно, не имеет и оптимального решения.

Случаи 1,2 и 3 для неограниченной ОДР приведены на рисунке 2.3 (варианты а,б,в).

На том же рисунке приведен случай 4 (вариант г).

 

                   х₂                 а                                                               х₂                      б                                               

                                                                                                     

 

                     

                                  CХ=Z 

                                      x₁                                                        x₁                                            

N                                                          N       CX=Z      

 

   x₂                    в                                x₂            г

                    CX=Z

 

         

N                    x_i                                                                                    x_i

 

Рис. 2.3

Таким образом, общая схема решения задачи ЛП должна предусматривать проверку совместности условий и ограниченности допустимой области и дальнейший выбор среди всех вершин многогранного выпуклого множества вершины, на которой достигается максимальное значение целевой функции.

2.4.  Некоторые понятия линейной алгебры и теории выпуклых множеств

Дальнейшие изучение свойств задачи ЛП требует использование ряда понятий и определений линейной алгебры и теории выпуклых множеств.

К ним относятся следующие понятия:

-  n-мерный вектор;

-  n-мерное векторное пространство;

-  линейная комбинация векторов;

-  линейная зависимость и линейная независимость системы векторов;

-  базис;

-  выпуклая линейная комбинация точек n-мерного пространства;

-  выпуклое множество;

-  крайняя точка.

Эти понятия рассмотрены в приложении А.

Рассмотрим далее каноническую задачу ЛП вида (2.4). Запишем ее в векторной форме, введя для каждого столбца матрицы А обозначение А_j, а для столбца свободных членов (вектора ограничений) обозначение В.