Теоретико-множественные понятия: Методические указания к практическим занятиям и СРС по курсу «Дискретная математика»

Министерство образованияРоссийской Федерации

Алтайский государственный технический университет

им. И.И. Ползунова

Кафедра

САПР

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ И СРС

ПО ДИСЦИПЛИНЕ

«ДИСКРЕТНАЯ МАТЕМАТИКА»

(Теоретико-множественные понятия)

Барнаул · 2001

УДК 519.6

И.В. Методические указания к практическим занятиям и СРС по курсу «Дискретная математика» для студентов специальности САПР. (Теоретико-множественные понятия) / Алт.гос.техн.ун-т им.И.И.Ползунова. – Барнаул: Изд-во АлтГТУ. – 2001. – 32 с.

Методические указания обеспечивают практические занятия и СРС по дисциплине «Дискретная математика», читаемого на кафедре «Системы автоматизированного проектирования» по теме «Теоретико-множественные понятия» в рамках автоматизированной системы поддержки преподавания.

Указания подготовлены кандидатом физико-математических наук доцентом

Рассмотрены и одобрены

на заседании кафедры САПР.

Протокол N 3 от 5 декабря 2000 г.

Рецензент: профессор

ã Алтайский государственный технический университет им

Методические указания

Структура учебного материала, расположенного на сервере кафедры:

-  методические указания (файл …\01_Topic\Instructions.rtf);

-  конспект лекции «Множества и их спецификации

(файл …\01_Topic\01_Summary.rtf);

-  задачи по материалу лекции «Множества и их спецификации»,

(файл …\01_Topic\01_Tasks.rtf);

-  конспект лекции «Отношения»

(файл …\01_Topic\02_Summary.rtf);

-  задачи по материалу лекции «Отношения»,

(файл …\01_Topic\02_Tasks.rtf);

-  конспект лекции «Отображения»

(файл …\01_Topic\03_Summary.rtf);

-  задачи по материалу лекции «Отображения»,

(файл …\01_Topic\03_Tasks.rtf);

-  конспект лекции «Функции»

(файл …\01_Topic\04_Summary.rtf);

-  задачи по материалу лекции «Функции»,

(файл …\01_Topic\04_Tasks.rtf);

-  литература для самостоятельной работы.

(папка …\01_Topic\Literature).

Для поиска литературы в электронной библиотеке рекомендуется применять каталог – файл library.mdb, устанавливаемый на кафедральном сервере. Ниже приведены ссылки на файлы этой библиотеки (компакт-диски  хранятся в методическом кабинете кафедры) и на файлы с литературой, отобранной из нее для работы с материалом данной темы.

Для экономии времени на занятиях далее приводится конспект лекций, который может служить опорой при освоении материала.

Литература

1.  Земзюлина В.Д., Литвинова М.В. Теория множеств. Комбинаторика. Высшая алгебра. – 1999.

(Library.99\BOOKS\rejhan.rar; Library.99\BOOKS\D_Math\Zemzjul.rar)

(…\01_Topic\Literature\Zemzjulina.rtf)

2.  Кук Д., Блейз Г. Компьютерная математика. – 1990.

(Libr_4.00\BOOKS\D_Math\Kuk\…)

(…\01_Topic\Literature\Cooke_Bez\…)

3.  Куликов Л.Я. Алгебра и теория чисел. – 1979.

(Library.00\BOOKS\D_Math\Kulikov\…)

(…\01_Topic\Literature\Kulikov\…)

4.  Калужнин Л.А. Введение в общую алгебру. – 1973.

(Libr_8.00\Books\Kalujnin\…)

(…\01_Topic\Literature\ Kalujnin \…)

5.  Кострикин А.И. Введение в алгебру. – 1977.

(Libr_4.00\BOOKS\D_Math\Kostrikin\…)

(…\01_Topic\Literature\ Kostrikin \…)

6.  Шнеперман Л.Б. Курс алгебры и теории чисел в задачах и упражнениях. Часть 1. – 1986. (Libr_4.00\BOOKS\D_Math\Chneperman\...)

(…\01_Topic\Literature\Shneperman\…)

7.  Зюзьков В.М. Дискретная математика. Часть 1. Теория множеств и математическая логика (Теория). – 1999.

(Libr_8.00\Books\Zuzkov\…)

(…\01_Topic\Literature\Zuzkov\…)

8.  Зюзьков В.М. Дискретная математика. Часть 1. Теория множеств и математическая логика (Варианты заданий). – 1999.

(Libr_8.00\Books\2_Zuzkov\…)

Множества и их спецификации

Конспект

Примеры множеств.

Георг Кант (1845-1918): «Множество или совокупность – это собрание определенных и различных объектов нашей интуиции или интеллекта, мыслимое в качестве целого».

, ; ; .

; .

·  .

·  ; , Исключим 6 из B, ,  задано некорректно.

·  ; , .

·  ; ,  .

·  ; рекурсивное определение,       , и т.д.

·  {множества, которые не являются элементами самих себя} - не существует.

 - обозначение множества  ( есть множество ). Если по предположению  - искомое множество, то или   или  . Рассмотрим два возможных случая.

а) . Тогда  удовлетворяет условию содержания, т.е. , и, следовательно, .

б)  говорит о том, что  не удовлетворяет условию вхождения в , и, следовательно, .

Следовательно, во всех случаях мы приходим к противоречию. Поэтому  не может существовать. Где же была сделана ошибка? Множества множеств, вероятно, разрешаются, и бесконечно большие множества также разрешаются; однако с «множеством всех множеств» нельзя работать в обычной теории множеств. Эта аномалия теории множеств известна как парадокс Рассела. Если мы уже имеем множество , то можно определить

.

Операции над множествами.

·   - пересечение,

·   - объединение.

, , , .

·   - разность.

·   - симметрическая разность.

·   - универсальное множество – множество рассматриваемых в данной задаче элементов.

·  Æ  - пустое множество,  Æ.

·   - дополнение множества  .

,  Æ.

·  ,  - мощность множества.

 - конечно  Æ или .

 - бесконечно  Æ.

Диаграммы Венна (Эйлера-Вейча)

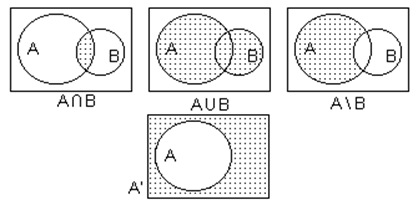
Подмножества.

·  .  .

Æ, , , для любого А.