Теоретико-множественные понятия: Методические указания к практическим занятиям и СРС по курсу «Дискретная математика», страница 2

·  .

. .

. .

. . . Æ. .

.  

ÆÆ.

.

·  à - булеан. ÆÃ; Ã.

Произведение множеств.

;  

Задачи

1.  Пусть , . Определить  в явном виде.

2.  Пусть  - множество целых чисел. Описать словами множество .

3.  Какие из следующих утверждений справедливы?

а) Æ; б) Æ; в) |{Æ}|=1; г) {{Æ}}{{{ Æ}}}; д) |{{Æ}}|=2.

4.  Проиллюстрировать диаграммами Венна следующие множества:

а) ; б) ; в) , где , , .

5.  Пусть даны множества , . Доказать, что

a)  ; б) ; в) ; г) .

6.  Доказать, что если , то Ã(A)ÍÃ(B).

7.  Доказать, что .

8.  Доказать, что .

9.  Доказать эквивалентность утверждений: , ,  Æ.

10.  Какие из следующих утверждений справедливы?

а) {Æ}Í Æ; б) Æ Í{Æ}; в) {Æ} Í{{Æ}}.

11.  Доказать, что при  и , .

12.  Доказать, что .

13.  Доказать, что для любых непустых конечных множеств  и  выполняются соотношения:

а) ÆÆ; б) ; в) ; г) ; д)  тогда и только тогда, когда .

14.  Записать возможные подмножества множества А={a, b, c}. Доказать, что для множества из n элементов существует 2ⁿ различных подмножеств.

15.  Даны множества U={0,1,2,3,4,5,…}, A={3*x: xÎU}, B={5*x: xÎU}. Записать АÇВ.

16.  Доказать, что, если АÈВ=А и АÇВ=А, то А=В.

17.  Рассмотрим класс А всех подмножеств множества U={00,01,10,11}, элементами которого являются пары, составленные из чисел 0 и 1. Элементами класса А являются, в частности, множества: H={00,01), Y={10,11}. Для класса А={Æ,H,Y,U} определить сложение и умножение.

18.  Доказать единственость пустого множества.

19.  Доказать равенство .

20.  Доказать равенство .

21.  Доказать равенство .

22.  Доказать равенство .

23.  Для произвольных совокупности множеств  и произвольного множества  доказать равенство .

24.  Для произвольных совокупности множеств  и произвольного множества  доказать равенство

25.  Для произвольных совокупности множеств  и произвольного множества  доказать равенство .

26.  Для произвольных совокупности множеств  и произвольного множества  доказать равенство .

27.  Доказать равенство .

28.  Доказать равенство .

29.  Перечислить все элементы каждого из множеств а) ; б) ; в) ; г) .

30.  Перечислить все подмножества множества А:

а); б); в).

31.  Вставьте между множествами символ  или символ :

а); б); в);

г); д) ; е) .

32.  Найти множество  из условия .

33.  Привести пример множеств  таких, чтобы выполнялись условия: .

34.  Пусть  и ,  доказать .

35.  Пусть  - не пустые, доказать а);

б) .

36.  Доказать равенство .

37.  Пусть , найти  из условий , .

38.  Доказать равенство .

39.  Пусть . Найти  из условий .

40.  Найти  из условий .

41.  Доказать, что .

42.  Доказать равенство .

43.  Доказать, что булеан пересечения двух множеств есть пересечение их булеанов.

44.  Найти  из условий .

Отношения

Конспект

Определения.

·  ; ,  - отношение; ; , ,

 - бинарное;

; .

·  Пример: , ;

.

·  ,  - тождественное, ;

 - универсальное, ;

.

·  ,  - область определения,

 - область значений.

·  Обозначения:  - отношения; , , .

·  ;

.

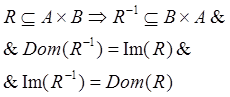Графическое представние.

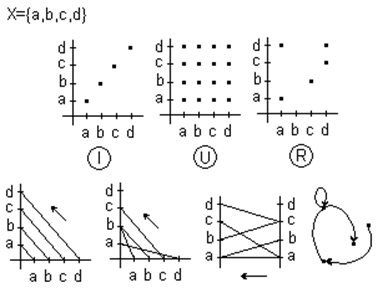
Свойства отношений.

·   - рефлексивно  .

·   - симметрично  .

·   - транзитивно .

·   - антисимметрично  .

·  Примеры:

;

;

.

 - рефлексивно, несимметрично, транзитивно, антисимметрично;

 - рефлексивно, несимметрично, транзитивно, антисимметрично;

  - рефлексивно, симметрично, нетранзитивно, неантисимметрично.

·  Симметричность и антисимметричность – не взаимноисключающие, .

Способы задания бинарных отношений.

·  Перечисление всех .

·  Матрицей     .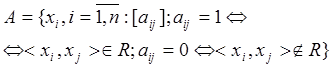

,  - матриц, способов индексирования.

·  Сечением  - верхнее;

 - нижнее.

.

;

.

; ;

.

Операции над бинарными отношениями.

,   .

·  Вложение, ;

; ;

;

.

·  Дополнение,

'     

  ;

 ;

; .

·  Пересечение ; объединение .