Теоретико-множественные понятия: Методические указания к практическим занятиям и СРС по курсу «Дискретная математика», страница 4

36.  Найти отношения для бинарного отношения , определенного на множестве целых чисел.

37.  Пусть  - бинарные отношения. Доказать .

38.  Найти отношения для бинарного отношения , определенного на множестве целых чисел.

39.  Для какого множества булеан линейно упорядочен относительно отношения ?

40.  Пусть  - антисимметричные отношения. Доказать  - антисимметричное отношение.

41.  Какими свойствами оно обладает бинарное отношение  перпендикулярна , определенное всех прямых плоскости?

42.  Найти композиции  и , где , .

43.  Какими свойствами оно обладает бинарное отношение , определенное на множестве всех подмножеств множества целых чисел?

44.  Найти композиции  и , где , .

45.   - бинарные отношения. Доказать .

46.   - бинарные отношения. Доказать .

47.  Какими свойствами оно обладает бинарное отношение , определенное на множестве действительных чисел?

48.  Найти отношения для бинарного отношения  делится нацело на и , определенного на множестве целых положительных чисел.

49.  Найти отношения для бинарного отношения  параллельна , определенное всех прямых плоскости.

50.  На множестве натуральных чисел задано бинарное отношение  «последняя цифра в десятиной записи числа  совпадает с последней цифрой числа ». Доказать, что  - отношение эквивалентности. Сколько элементов в фактор-множестве ?

51.  Пусть  -непустое конечное множество, на подмножествах которого определено отношение  «число элементов в  меньше или равно числу элементов в . Является ли  отношением частичного порядка?

52.  Перечислить линейные порядки на множествах .

53.  Доказать, что отношение  есть отношение эквивалентности на  (- множество вещественных чисел). Найти классы эквивалентности и изобразить их на плоскости.

Отображения.

Конспект

·  ; образ: ;

прообраз:

.

· 

-  сюрьективно  

-  инъективно  ;

-  биективно  сюрьективно & инъективно.

·    ;

·  , ; , .

·  сужение:   .

·  Суперпозиция: , ,  ;

, , левый, правый, двухсторонний;

;

, ;

;  .

·  Теорема: - обратимо    - биективно.

Теорема:    &  

 , .

Теорема:    & .

Теорема:  &  

  &

·   преобразование.

Теорема:     

·  ;   , ;

 - отношение эквивалентности.

,  - естественное;

, - фактор-множество.

Факторизация: .

:     

.

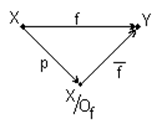
Теорема:  - единственно.

·  , ,  - подстановка,  - биекция; .

Композиция подстановок, циклическая подстановка, разложение на циклы, произведение циклов.

·  Операции:  - бинарная,  - -местная, унарная;

Таблица Кэли; коммутативность.

·  ; ; ассоциативность, коммутативность, дистрибутивность, единица, обратный элемент, идемпотентный элемент.

Задачи

1.  Доказать:  обратимо  .

2.   &   &  . Доказать.

3.     & . Доказать.

4.   &   & . Доказать.

5.   &   . Доказать.

6.  ,  - естественное   - единственное. Доказать.

7.   - координатная плоскость;

  .

8.    Построить различные фактормножества.

9.   Построить различные фактормножества.

10.  Описать  задачи 7.

11.  Определить частичный порядок на булеане 4-х элементного множества.

12.  Определить отношение частичного порядка на множестве делителей 24. Построить диаграмму.

13.  Построить все сюрьективные отображения множества  на множество .

14.  Найти все отображения множества  в себя, указать среди них инъективные и сюрьективные.

15.  Пусть  - конечное множество,  - будеан . Определим  следующим образом , где , если  и , если . Доказать, что  - биекция.

16.  Какие отображения ниъективны, сюрьективны?

-   ;

-   ;

-   ;

-   ,  - множество целых чисел;

-   ;

-    - булеан,  - конечное множество.

17.  Доказать, что  инъективно тогда и только тогда, когда для любых  и  .

18.  На множестве  всех отображений  в  определено отношение   для одних и тех же значений . Доказать, что  - отношение эквивалентности, найти классы эквивалентности.