Теоретико-множественные понятия: Методические указания к практическим занятиям и СРС по курсу «Дискретная математика», страница 5

19.  Пусть  Определим  так, что .

Доказать .

20.  На множестве  всех отображений  в  определено отношение  . Является ли  - отношением частичного порядка?

21.  Найти , где  для следующих отображений

-  ;

-  .

22.  Даны отображения   и . Найти  и .

23.  На множестве  всех отображений  в  определено отношение  . Является ли  - отношением частичного порядка?

24.  Даны отображения   и . Найти  и .

Функции

Конспект

Определение.

·   ,  - бинарное отношение.

 - функция    

  

.

Обозначения: ; ; .

 - действительная (вещественная), .

·  ;   ,

; Ã.

;

; ; .

Счетные множества.

·  Счетность, вычислимость. ; “1”, “+”?

, , ,…;

, , ,…;

.

.

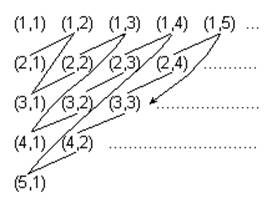
·  Теорема: .

 

  

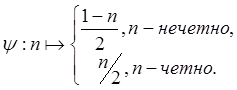
·  Теорема: .

,

 

 .

;

,

,   .

  .

·  Теорема: ;

, .

Противное: все числа из  можно пронумеровать,

 - -е число.

Построим новое: , ;

 отсутствует среди пронумерованных, противоречие.

, для общности - .

·  Подстановки: , ,   

. . .

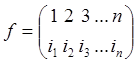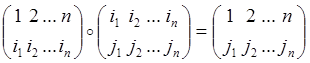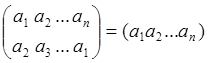.  - циклическая подстановка;     .

Теорема: Каждая подстановка может быть представлена в виде непересекающихся циклов.

·  Последовательность : , ,

,

 - n-й член последовательности.

·  Функционал: , ,  ,.

, ,   .

Аналитические свойства вещественных функций.

·  Последовательность , ,

·  Предел :

;  - предел;

,  - сходится;  - нет предела  

 - расходится.

,  , , ,

тогда .

 - расходится.

, ,

, , ,

  ,  .

,  - ряд,  - -я частичная сумма,

.

·  Непрерывность. , .

  

.

Пример. .

Поскольку   

.

Следовательно, .

Если выбрать , то .

      

 .

; .

  .

  .

Примеры. ;

.

, , ;

;

;

;

.

·  Дифференцируемость:  .

, .

  

  .

 &   

.

  .

    

, , .

, , ,

.

  .

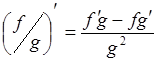 и т.д.

·  Интегрирование. , , ,

; .

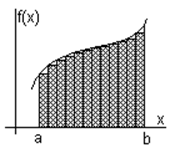
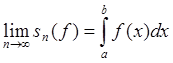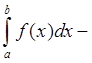 интеграл Римана,

Свойства:   

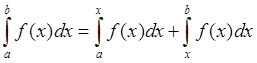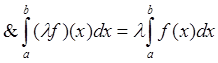,   и

.

   .

 и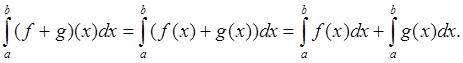

Доказательство: ,  

Теорема. ,

   

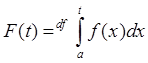
Доказательство: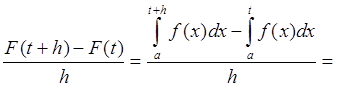

.

  .

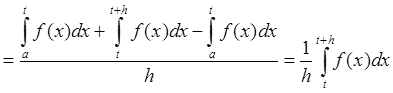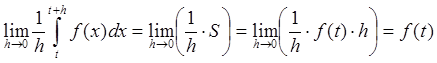
Пусть  .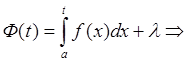

Определим  .

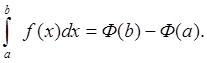
 - класс эквивалентности или неопределенный интеграл.

Задачи

1.  .

2.  .

3.  .

4.  , . Доказать

5.  , Доказать .

6.  , , , , . Доказать .

7.  Доказать формулу для .

8.  Доказать формулу для .

9.  Доказать формулу для .

10.  ,

11.  ,

12. 

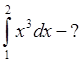
13. 

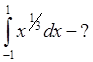
14. 

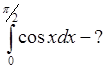
15. 

16. 

17. 

18.  * - операция ? , .

19.  * - операция ? , .

20.  * - операция ? , .

21.  * - операция ? , .

22.  * - ассоциативная операция ? , .

23.  * - операция на  .

Доказать .

Содержание                                                                                  стр.

Методические указания                                                                    3

Литература                                                                                          3

Множества и их спецификации                                                       4

Конспект                                                                                        4

Задачи                                                                                            7

Отношения                                                                                    …10

Конспект                                                                                  …10

Задачи                                                                                      …15

Отображения                                                                                …19

Конспект                                                                                  …19

Задачи                                                                                      …21

Функции                                                                                         …23

Конспект                                                                                  …23

Задачи                                                                                      …30