Решение дифференциальных уравнений и систем дифференциальных уравнений средствами Mathcad и Maple

Ленинградский государственный университет им .А. С. Пушкина.

Кафедра информатики и вычислительной техники

КУРСОВАЯ РАБОТА

по дисциплине: математическое моделирование

на тему: Решение дифференциальных уравнений и систем дифференциальных уравнений средствами Mathcad и Maple

выполнила: студентка 4 курса

Царицына Мария

проверила:

Содержание

Введение……………………………………………………..3

Глава 1………………………………………………………..7

П. 1 Формулировка заданий…………7

П. 2 Необходимые сведения…………7

Глава 2……………………………………………………….16

П. 1 Решение системы ДУ…………..16

П. 2 Решение задачи…………………36

Список литературы………………………………………….42

Введение

 П.1 Моделирование. 

Моделирование – построение моделей реально существующих объектов, замена реального объекта его подходящей копией, исследование объекта познания на его модели.

Можно моделировать внешний вид, структуру, поведение. Внешний вид моделируется с целью идентификации, долговременного хранения, для сравнения. Структура моделируется с целью изучения свойств объектов, выявления значимых связей, изучение стабильности объекта. Поведение моделируется с целью прогнозирования, управления, выявления причинно- следственных связей, установление связи с другими объектами.

Классификация – распределение объектов по классам в зависимости от их общих признаков, фиксирующие закономерные связи между классами объектов.

Классификация моделей.

1.  по сущности все модели делятся на 3 класса:

a)  материальные – реальные объекты;

b)  воображаемые;

c)  информационные – это в той или иной форме описание объекта моделирования, в которой отражаются знания человека об объекте моделирования;

2.  по сферам  деятельности субъекта моделирования:

a)  познавательные;

b)  коммуникативные;

c)  в сфере практической деятельности;

3.  по характеристике объекта моделирования:

a)  по внешнему виду;

b)  по структуре;

c)  по поведению;

4.  по роли управления объектом:

a)  регистрирующие;

b)  эталонные;

c)  прогностические;

d)  имитационные;

e)  оптимизационные;

5.  по степени формализации:

a)  неформализованные;

b)  частично формализованные;

c)  формализованные;

d)  на формальном языке;

6.  по учету фактора времени:

a)  статические;

b)  динамические;

7.  по фактору неопределенности:

a)  детерминированные;

b)  стохастические;

П.2  Приложения   MATHCAD и  MAPLE.

Пакеты математических программ созданы для самых разнообразных вычислений и вычерчивания графиков. В них процесс вычислений сильно автоматизирован, что позволяет экономить время на программировании.

В системе MATHCAD автоматизированы не только вычисления, но и сам процесс программирования , так что можно не знать ни численных методов, ни языков программирования.

В появляющемся окне можно писать необходимые  выражения так, как они пишутся в алгебре. При этом можно пользоваться знаками суммы, интеграла, производной и целым рядом других. Эти знаки вводятся с помощью кнопок в меню, которое имеется на краю экрана.

Если в задаче требуется использовать несколько формул, нужно иметь в виду, что каждой формуле отводится определенный шаблон – прямоугольник. Закончив написание одной формулы, нужно отойти клавишей курсора вправо или вниз от предыдущего шаблона. Теперь можно набирать следующую формулу и т. д.

В любом месте экрана можно писать комментарии, вызвав Вставка – Текстовая область.

Для ввода значения какой – либо величины надо написать а:=45. Если в следующем шаблоне набрать у:=а/а*2, то вычисления происходят сразу после отхода от написанного блока.

Для вывода значения, например, у надо набрать в следующем шаблоне у= (без двоеточия).

Ошибочные записи система высвечивает красным и дает краткое пояснение. Надо вернуться и исправить запись.

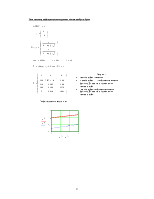
Большим преимуществом системы является возможность оперировать не только скалярными величинами, но и векторами и матрицами. Причем под вектором понимается одномерный массив чисел, а под матрицей – таблица чисел в m строк и n столбцов.

Функция вводится просто написанием формулы у(х):=х*4/(17-х). После этого можно написать у(0.1)= и получить значение у в данной точке.

Можно решать уравнения и системы уравнений.

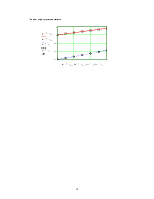
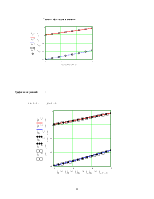
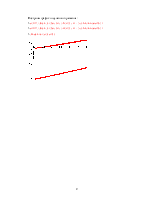
Сильно автоматизировано вычерчивание графиков. В системе организовано автомасштабирование.

Зацепляясь с помощью мыши за края шаблона, можно увеличить график, выделив  его, переместить в другое место. График можно переформатировать( изменить цвета линий, ввести сетку, ввести логарифмический масштаб и т. д.).