Решение дифференциальных уравнений и систем дифференциальных уравнений средствами Mathcad и Maple, страница 7

> e2:=odeplot(v,[x,y2(x)],2..5,color=green,thickness=6):

> e3:=odeplot(p,[x,y1(x)],2..5,color=black,linestyle=3,style=point):

> e4:=odeplot(p,[x,y2(x)],2..5,color=black,style=point,symbol=box):

> e5:=plot([o1,o2]):

> display(e1,e2,e3,e4,e5);

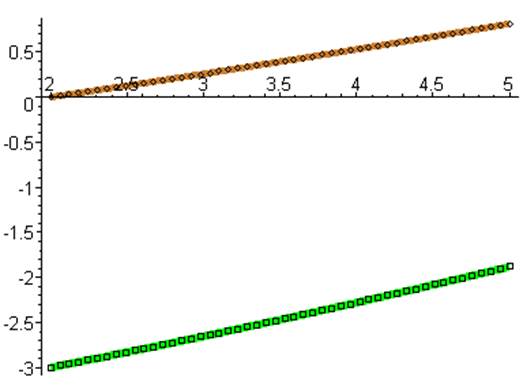
Задание 2.

Задание 2.

Построить математическую модель задачи, решить задачу математически и символьно в MATHCAD или  MAPLE , решить численно в MATHCAD и  MAPLE(любым методом). Построить графики полученных решений. Оценить погрешность численного решения, сравнив его с точным решением, найденным аналитически.

Задача:

Катер движется в спокойной воде со скоростью 10 км/ч. На полном ходу его мотор был выключен, и через 20 секунд скорость катера уменьшилась до 6 км/ч. Считая, что сопротивление воды движению катера пропорционально его скорости, найти:

·  скорость катера через 2 минуты после остановки мотора.

расстояние, пройденное катером в течение первой минуты после остановки мотора.

1.Построим математическую модель.

Из курса математического анализа мы знаем, что ускорение задается как dv/dt, поэтому, согласно условию задачи, составляем дифференциальное уравнение:

Разделим обе части уравнения на v и умножим на dt:

Получим систему уравнений:

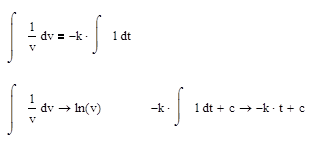откуда получаем: ln(v)=-k*t+c

нам дано начальное условие: v0=10, откуда:

подставим полученное значение с:

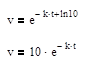
выразим коэффициент к, учитывая, что нам дано время v1=1/180:

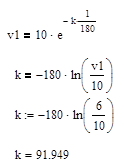
теперь мы можем найти скорость катера через 2 минуты, после остановки мотора:

проинтегрируем функцию:

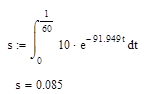
получили расстояние, пройденное катером в течение первой минуты после остановки мотора.

2.Символьное и численное решение в системе Maple.

> LO:=diff(x(t),t$2)+k*diff(x(t),t$1)=0;

Задали дифференциальное уравнение, теперь решим его:

> dsolve(LO,x(t));

Решим задачу Коши, определим общее решение:

> dsolve({LO,x(0)=0,D(x)(0)=10},x(t));

Определяем вспомогательный элемент kk, равный k :

> S:=t1->(10/k1)*(1-exp(-k1*t1));

> v1:=t1->D(S)(t1);

> t0:=1/180;

> v1:=k1->10*exp(-k1*t1);

> kk:=fsolve(10*exp(-k1*1/180)=6,k1=0..100):kk;

Найдем скорость катера через 2 минуты после остановки:

> t1:=1/30:k:=kk:v:=v1(k);

> SS:=int(10*exp(-t*kk),t=0..1/60);

Проверим решение, решив задачу численно:

> k:=kk:

> Res:=dsolve({LO,x(0)=0,D(x)(0)=10},x(t),type=numeric);

> for _i from 0 to 1/30 by 1/360 do Res(_i);end do;

Получаем, что скорость катера через 2 минуты также равна  , а расстояние, пройденное катером в течение первой минуты после остановки  равно

> with(plots):

> sp:=odeplot(Res,[t,x(t)],0..1/30):

> display(sp);

>

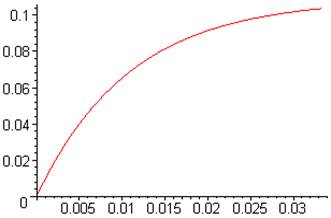
3.Численное решение и оценка погрешности в системе MATHCAD.

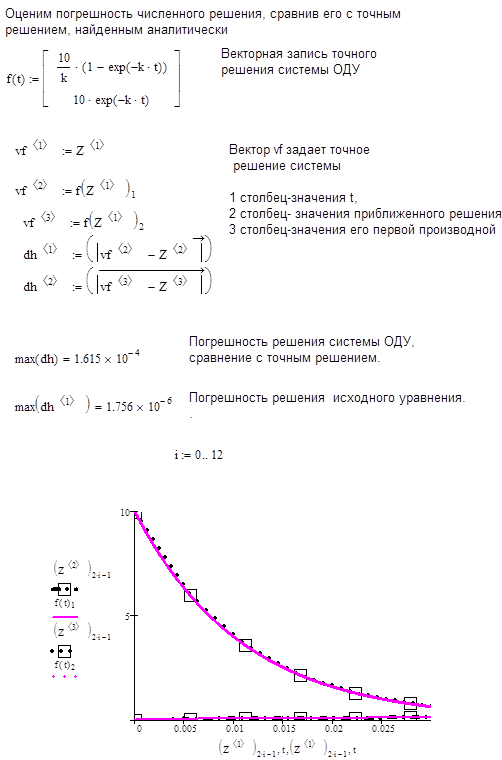Список литературы.

1.  Г. А. Бордовский Э. В.Бурсиан

Общая физика: курс лекций с компьютерной поддержкой: уч. Пособие для студентов высших учеб Заведений: В 2т. М: 2001.(том 1, том 2);

2.  Н. М. Матвеев

Методы интегрирования обыкновенных дифференциальных уравнений.

СПб.: 2003.

3.  В. М. Вержбицкий.

Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М: 2001.

4.  Т. А.Алексеева

Компьютерное моделирование в пакете MATHCAD (дифференциальные уравнения). Учебное пособие.  СПб.: 2003;

5.  Т. А. Алексеева

Информационные технологии в математике(система MATHCAD). Учебное пособие. СПб. : 2003;

6.  Т.А.Алексеева, А. А. Жихарева

Информационные технологии в математике(система Maple). Учебное пособие. СПб.:2003.