Решение дифференциальных уравнений и систем дифференциальных уравнений средствами Mathcad и Maple, страница 4

Пусть на отрезке [a, b]  требуется найти численное решение уравнения 1-го порядка.

Вычисления проходят в 3 этапа:

1.  Вычисляют 4  значения вспомогательных элементов.

2.   Рассчитывается значение sу.

3.  Рассчитывается искомое значение у.

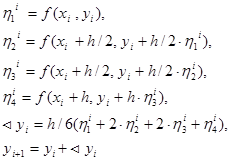
Шаг выбирают таким образом, чтобы значение h⁴  было меньше нужной точности.

·  Метод Эйлера по рекуррентным формулам.

Рассмотрим дифференциальное уравнение 1 порядка  с начальным условием.

Решить дифференциальное уравнение численным методом, это значит для заданной последовательности аргументов x0,x1,…,xn и числа y0, найти такие значения y1, y2,…,yn, чтобы выполнялось условие:

Последняя формула носит название формулы Эйлера.

Разобьем отрезок интегрирования на n равных частей, получим последовательность точек х0, х1,…хn , где x_i+1-x_i=h

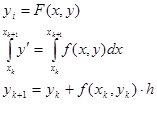h=(b-a)/n

·  Метод Булирша- Штерра.

Реализация решений средствами MATHCAD и  MAPLE.

Система MATHCAD предоставляет широкие возможности для реализации различных видов дифференциальных уравнений и их систем:

·  встроенные функции для численного решения

·  вычисление решений по итерационным формулам

·  вычисление аналитических решений по готовым формулам

·  использованием преобразования Лапласа для решения уравнений в частных производных

·  запись алгоритма решения с помощью средств программирования системы MATHCAD.

Встроенные функции.

Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы, по крайней мере, следующие величины, необходимые для поиска решения – начальные условия; набор точек, в которых нужно найти решение; само дифференциальное уравнение, записанное в некотором специальном виде.

Для решения любого ОДУ в форме Коши (или системы ОДУ) необходимо представить его в виде системы ОДУ 1-го порядка и записать в векторной форме.

Замечание:

одиночное ОДУ 1-го порядка является частным случаем системы ОДУ 1-го порядка, и векторная форма в этом случае вырождается в скалярную функцию с вектором начальных условий в виде одной точки;

Функция rkfixed (y,x1,x2,n,D)

предназначена для решения систем ОДУ в форме Коши методом Рунге – Кутта четвертого порядка с фиксированным шагом.

Аргументы функции:

·  у – вектор начальных условий размерности n, где n – порядок ОДУ или число уравнений в системе уравнений (если решается система). Для ОДУ 1-го порядка вектор начальных условий вырождаются в одну точку у0.

·  x1, x2 – граничные точки интервала, на котором ищется решение ДУ. Начальные условия, заданные в векторе у,– это значение решения в точке х1.

·  n – число точек(не считая начальной точки), в которых ищется приближенное решение. Число строк в матрице, возвращаемой функцией равно  n+1.

·  D(x, y) – вектор-функция, состоящая из n элементов и содержащая первые производные искомых функций, т. е. правые части системы ОДУ, представленных в нормальной форме. Для ОДУ 1-го порядка вырождается в скалярную функцию.

В результате решения получается матрица, состоящая из n столбцов, где первый столбец содержит точки, в которых ищется приближенное решение, оставшиеся столбцы содержат:

·  для ОДУ 1-го порядка: значения найденного приближенного решения у(х) в соответствующих точках первого столбца;

·  для ОДУ высшего порядка: значения у(х), y’(х), y’’(x), …,y^(n-1)(x) в соответствующих точках первого столбца; 

·  для системы ОДУ 1-го порядка: значения найденных приближенных решений в соответствующих точках первого столбца;

·  для системы ОДУ высшего порядка: значения решений и их производных, соответствующие точкам из первого столбца; порядок, в котором выводятся решение и его производные, повторяет порядок их расположения в функции D(x, y) и векторе начальных условий у.