Линейные дифференциальные уравнения. Одноканальная динамическая система

Линейные дифференциальные уравнения

Лекция 2

      Одноканальная динамическая система

Прежде, чем перейти к  изучению управления и управляемости, нам необходимо вспомнить основные правила построения решения линейных дифференциальных уравнений и систем, содержащих п уравнений первого порядка

Рассмотрим линейное уравнение с постоянными коэффициентами

                                  (2.1)

Из теории дифференциальных уравнений известно, что общее решение уравнения складывается из общего решения однородного уравнения (без правой части) и частного решения неоднородного. Однородное уравнение

                                              (2.2)

имеет решение, которое можно записать в виде линейной комбинации экспоненциальных функций , где - корень характеристического уравнения       

                                       (2.3)

Это уравнение имеет п корней. Пусть среди них имеется  т  действительных и п-т  комплексно-сопряжённых:

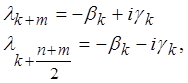
                                                  (2.4)

Решение однородного уравнения, в этом случае, можно представить суммой

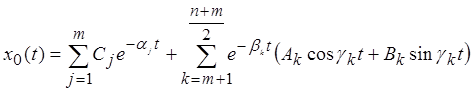.                   (2.5)

Постоянные  определяются из начальных условий общего решения уравнения (2.1)

Динамическая система, которая подчиняется дифференциальному уравнению (2.1) является асимптотически устойчивой, если его решение при любых начальных условиях при отсутствии внешнего возбуждения асимптотически стремится к нулю. Отсюда следует, что условие асимптотической устойчивости эквивалентно требованию      или, что  то же самое,    .

Частное решение уравнения с правой частью при нулевых начальных условиях определяет интеграл-свёртка

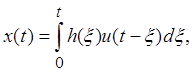                                                               (2.6)

где h(x) – функция, которая зависит только от коэффициентов дифференциального уравнения, носит название импульсной характеристики. Это название объясняется тем, что при воздействии на систему единичного импульса её отклик будет тождественен импульсной характеристике.

Пусть       тогда

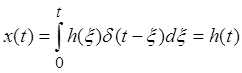
Нетрудно установить, что импульсная характеристика подчиняется однородному дифференциальному уравнению системы

                                            (2.7)

и удовлетворяет начальным условиям

.

Итак, общее решение уравнения (2.1) имеет вид

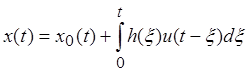 .                                                   (2.8)

При асимптотической устойчивости выполняется условие

Таким образом, с увеличением времени влияние начальных условий на решение ослабевает. В результате получим решение, которое зависит только от функции