Сигналы
Аппроксимация сигналов
Под дискретным сигналом понимается последовательность вещественных чисел:
S1, S2, ….. SN, где Si- i- отсчет сигнала.
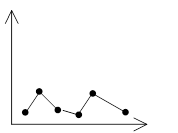
Предполагается, что временные интервалы между сигналами одинаковы, т.е. частота дискретизации одинакова.
Если сигнал поступает после аналого-цифрового преобразователя (АЦП), то Si – целые числа в диапазоне [0,255] – для 8-разрядного АЦП;
[0,1025] – для 10-разрядного АЦП.
С точки зрения программирования сигнал рассматривается как массив.
Аппросимация сигналов представляет собой замену последовательности сигналов S1, S2, ….. SN отрезками полиномов.
Как правило, используются полиномы 0-го, 1-го, 2-го порядка или кубический сплайн.
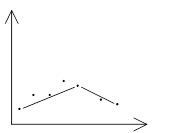
Аппроксимация позволяет решить 2 задачи:
- сжатие сигнала (уменьшение объема памяти для его хранения);
- выделение структурных особенностей.
Найти min или max сложно. После аппроксимации их выделение достаточно просто.
Для сжатия сигналов используются также методы полностью сохраняющие информацию сигнала.
Обычные архиваторы мало эффективны для сжатия сигналов, т.к. в реальных сигналах практически нет повторяющихся участков. Наиболее распространенным методом сжатия сигналов является метод разностного кодирования.
Разностное кодирование.
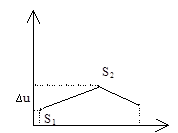
Разность между соседними отчетами 
меньше
уровня сигнала, что позволяет уменьшить разрядность для отчетов.
Первый отчет хранится целиком, далее хранятся разности отчетов. При этом уменьшается размерность разрядной сетки.
S1, 
=S2-S1,
=S2-S1, 
=Sk+1-Sk.
Если выходит за
размерность разрядной сетки, то определенный код (ПРЕФИКС), то это
означает, что дольше идет сам отчет.
|
префикс |
|
|
11111….11 |
Sk |
Лабораторные работы.
Если отчеты – это это последовательность байтов: S1,
S2, ….. SN,
то для хранения разностей используется - 4
бита.
Префикс определяют обычно как код 15 (1111b) [-7…0 …7].
<S1>, <>……
<префикс><Sk>…
Степень сжатия сигнала определяется:
(с потерей информации)
К ним относятся следующие методы аппроксимации:
1. Фиксированная апертура.
2. Экстраполяция нулевого порядка.
3. Интерполяция нулевого порядка.
4. Экстраполяция первого порядка.
5. Интерполяция первого порядка.
6. AZTEC.
7. МНК (метод наименьших квадратов).
Методы 1-6 используют полином 1-го и 2-го порядка и достаточно просты для их использования в реальном масштабе времени, т.е. одновременно с снимаемым сигналом вести аппроксимацию.
1. Фиксированная апертура.
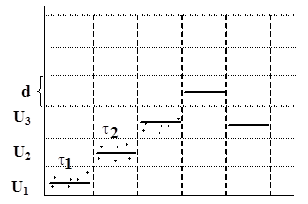
В каждом диапазоне сигнал
заменяется отрезком, т.е. сигнал заменяется последовательностью горизонтальных
отрезков: 
(1 байт; 1 байт).
d – апертура.
Методы аппроксимации характеризуются величиной ошибки восстановления сигнала.
Пусть S(t)- исходный сигнал, 
-аппроксимируемый.
Тогда ошибка вычисляется двумя способами:
1.
.
2. Среднеквадратичная ошибка равна сумме квадратов отклонений:
.
1 и 2 подсчитать для каждого метода. d-свободный параметр (подсчитать самостоятельно).
2. Экстраполяция нулевого порядка.
Экстраполяция нулевого порядка: S1 – становится центром уровня U1, пока последующие отчеты остаются внутри интервала уровень не меняется.
[ U1-d/2; U1+d/2].
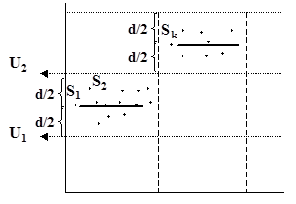Иначе Sк –
определяет уровень U2 и т.д.
3. Интерполяция нулевого порядка.
Пусть имеются К- отчетов сигналов внутри коридора.
Определяются max и min отчеты.
Текущий уровень определяется по среднему значению:
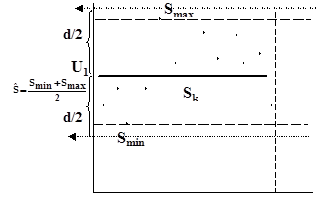При поступлении Sк+1 пересчитываются Smax,
Smin, Sсредн. Если все S1,…. Sк+1 находятся внутри
нового коридора (
), берем следующий S2.
В интерполяции 0-го порядка уровень определяется Smax, Smin, Sсредн. на данном отрезке.
4. Экстраполяция 1-го порядка.
Здесь используются полиномы 1-ой степени или отрезки наклонных кривых.
Способ хранения отрезков следующий: хранятся разности между концом и началом отрезков u0, u1, u2, … um.
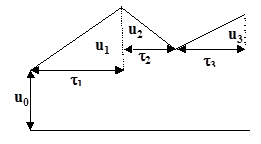
Т.е., в памяти хранится массив:
u0, <u1,t1>, <u2,t2>…
Отрезок [S1,S2] – определяет наклонный коридор.
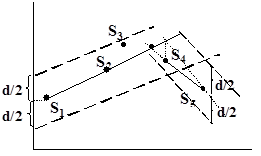
Берутся отчеты, пока они находятся внутри коридора, как только текущий отчет Sк выходит за пределы этого коридора, то формируется новый отрезок [Sк-1, Sк] – теперь он определяет новый коридор, и т.д.
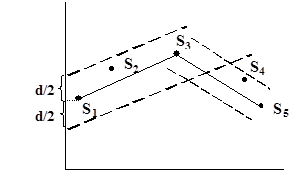
5. Интерполяция 1-го порядка.
Соединяются S1 и S3 , если S2 лежит внутри коридора, то соединяются S1 и S4, если S2 и S3 – находятся внутри, то соединяются S1 и S5, и т.д.
Если существует К, такое что Sк не попадает в коридор, то Sк-1 становится началом нового отрезка [Sк-1, Sк+1].
6. Алгоритм AZTEC.
Выполняет аппроксимацию, состоящую из последовательности полиномов 0-ой степени и полиномов 1-ой степени.
Полиномы 0-ой степени называются ЛИНИЯМИ.
Полиномы 0-ой степени называются СКЛОНАМИ
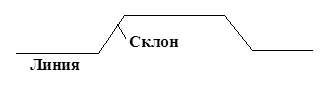
Сначала выполняется аппроксимация горизонтальными отрезками, а затем при выполнении некоторых условий часть горизонтальных отрезков заменяется наклонными.
На первом шаге выполняется интерполяция 0-го порядка.
Линия длина которой больше > а (некоторый параметр алгоритма, который нужно подбирать), называется ПЛАТО.
Пусть ui-1, ui, ui+1 – три соседних уровня отрезка.
Отрезок ui называется экстремумом, если выполняется условие:
(ui - ui-1 )(ui+1-ui)<0
Очевидно, что экстремум представляет собой :
Плато + Экстремум = Граница.
Пусть L0, L1, … , Ln –последовательность линий, причем L0, Ln - границы.
Остальные линии границами не являются, тогда L1, L2, … , Ln-1 заменяются СКЛОНОМ.
Uсклона = Ln - L0.
отрезки хранятся как массив (ti, ui).
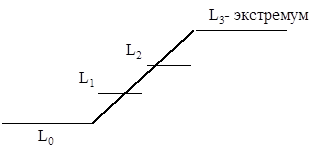
В алгоритме AZTEC линии склонов хранятся в виде пар (ti, ui), величины ti для склонов берутся отрицательные (ti<0).
7. Метод наименьших квадратов.
Требования к выполнению лабораторных работ:
1. Реализовать методы.
2. Распечатать сами сигналы.
3. Распечатать их аппроксимации.
4. Вычислить степень сжатия.
5. Подобрать параметры алгоритма d, a - такие, чтобы сигнал сохранял все особенности при максимальном сжатии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
