Нормальной системой дифференциальных уравнений
называется система в ![]() вида
вида
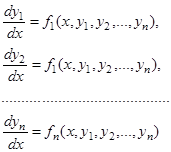 (1)
(1)
Здесь ![]() – искомые функции,
– искомые функции, ![]() – независимая переменная,
– независимая переменная, ![]() – заданные функции.
– заданные функции.
Введя в рассмотрение векторы
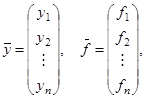
можем записать систему (1) в векторной форме
![]() .
(1/)
.
(1/)
Задача Коши для системы (1) или (1/) ставится следующим образом: найти решение системы, удовлетворяющее начальному условию
![]() (2)
(2)
или
![]() (2/)
(2/)
Теорема (существование и единственности решения задачи Коши
для нормальной системы). Пусть все функции ![]() непрерывны
вмести со своими частными производными
непрерывны
вмести со своими частными производными ![]() в
некоторой области
в
некоторой области ![]() , содержащей точку
, содержащей точку ![]() . Тогда существует интервал
. Тогда существует интервал ![]() и единственный набор дифференцируемых
функций
и единственный набор дифференцируемых
функций ![]() , определенных на этом интервале, являющихся
решением системы (1) на
, определенных на этом интервале, являющихся
решением системы (1) на ![]() и удовлетворяющих
начальным условиям (2).
и удовлетворяющих
начальным условиям (2).
Общее решение системы (1) представляет собой совокупность ![]() функций
функций ![]() таких,
что
таких,
что ![]() – решение системы и при этом по
начальному условию (2) можно указать единственный набор
– решение системы и при этом по
начальному условию (2) можно указать единственный набор ![]() такой,
что
такой,
что ![]() .
.
Заметим, что любое уравнение ![]() -го
порядка
-го
порядка ![]() может быть сведено к нормальной системе
дифференциальных уравнений вида (1). Действительно, полагая
может быть сведено к нормальной системе
дифференциальных уравнений вида (1). Действительно, полагая ![]() , получим
, получим
![]() .
(3)
.
(3)
Система (3) есть частный случай системы (1).
Отметим, что сведение нормальной
системы к одному дифференциальному уравнению ![]() -го
порядка возможно далеко не всегда. Случаи, когда такое сведение возможно, будут
рассмотрены ниже.
-го
порядка возможно далеко не всегда. Случаи, когда такое сведение возможно, будут
рассмотрены ниже.
Линейные системы дифференциальных уравнений. Общая теория.
Линейной системой называют нормальную систему дифференциальных уравнений вида
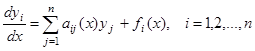 (4)
(4)
Если в формуле (4) все ![]() , то система называется однородной.
, то система называется однородной.
Также как и для линейного уравнения ![]() -го порядка можно показать, что условия
теоремы Коши для системы (1), в которой все входящие в нее функции определены
на интервале
-го порядка можно показать, что условия
теоремы Коши для системы (1), в которой все входящие в нее функции определены
на интервале ![]() , сводятся к требованию непрерывности
, сводятся к требованию непрерывности ![]() на этом интервале. При этом решение с
начальными условиями
на этом интервале. При этом решение с
начальными условиями ![]() для произвольных
для произвольных ![]() и
и ![]() продолжаемо
на весь интервал
продолжаемо
на весь интервал ![]() .
.
В дальнейшем, кроме обычных операций матричной алгебры, нам понадобятся операции дифференцирования и интегрирования матриц.
Производной от матрицы ![]() называется матрица
называется матрица ![]() . Интеграл от матрицы определяется так:
. Интеграл от матрицы определяется так:
 .
.
Используя матричные обозначения, запишем систему (4) в виде
![]() .
(6)
.
(6)
Начальные условия в матричной форме будут иметь вид (2/).
Однородная система
Пусть ![]() . Тогда получим однородную систему
. Тогда получим однородную систему
![]() (7)
(7)
Пусть задано ![]() столбцов
столбцов
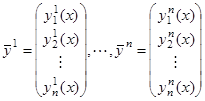 .
.
Составим из них матрицу
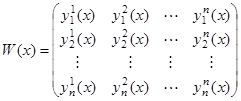 (8)
(8)
Наряду с уравнением (7), левая и правая часть которого суть вектор-столбцы, рассмотрим уравнение
![]() ,
(9)
,
(9)
левая и правая часть которого –![]() матрицы.
матрицы.
Теорема 1. Если ![]() – решения уравнения
(7), тогда матрица
– решения уравнения
(7), тогда матрица ![]() , определенная формулой (8),
есть решение матричного уравнения (9). И обратно, если
, определенная формулой (8),
есть решение матричного уравнения (9). И обратно, если ![]() –
решение матричного уравнения (9), то каждый столбец этой матрицы есть решение
уравнения (7).
–
решение матричного уравнения (9), то каждый столбец этой матрицы есть решение
уравнения (7).
Для доказательства справедливости утверждения теоремы 1 достаточно расписать уравнение (9) поэлементно.
Столь же просто можно убедиться в справедливости следующего утверждения.
Теорема 2. Если ![]() – решение уравнения
(9), то
– решение уравнения
(9), то ![]() , где
, где ![]() ,
будет решением уравнения (7), а
,
будет решением уравнения (7), а ![]() , где
, где ![]() -матрица, также будет решением уравнения
(9).
-матрица, также будет решением уравнения
(9).
Определение. Будем говорить, что вектор-функции ![]() линейно зависимы на интервале
линейно зависимы на интервале ![]() , если существуют постоянные
, если существуют постоянные ![]() не все равные нулю такие, что
не все равные нулю такие, что
![]() .
(10)
.
(10)
Если из соотношения (10) следует, что ![]() , то вектор-функции
, то вектор-функции ![]() линейно независимы на
линейно независимы на ![]() .
.
Пусть матрица ![]() определена
формулой (8),
определена
формулой (8), ![]() . Тогда соотношение (10)
принимает вид
. Тогда соотношение (10)
принимает вид
![]() (10/)
(10/)
Определение. Функциональный определитель ![]() называют
определителем Внонского (вронскианом) системы вектор-функций
называют
определителем Внонского (вронскианом) системы вектор-функций ![]() .
.
Теорема 3. Если решения ![]() уравнения
(7) линейно зависимы на интервале
уравнения
(7) линейно зависимы на интервале
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.