Дифференциальные уравнения: методы решений с примерами

Функция называется однородной измерения т, если для любых t выполняется тождество

Дифференциальное уравнение первого порядка

называется однородным, если и однородные функции одного и того же измерения.

С помощью новой переменной и, вводимой по формуле

однородное уравнение приводится к уравнению с разделяющимися переменными.

Пример 1. Найти общий интеграл уравнения

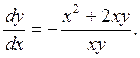
Применим подстановку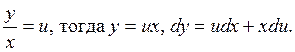

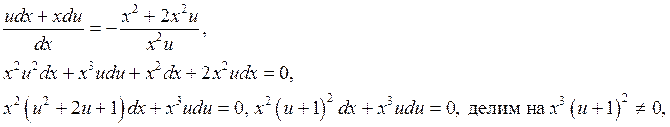
получаем:

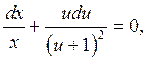интегрируем

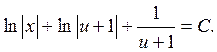
Делая обратную замену функции, получаем окончательный ответ:

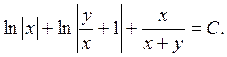
Пример 2. Найти частное решение уравнения 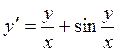при начальном условии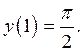

Произведём замену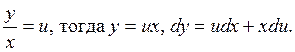

В результате получаем

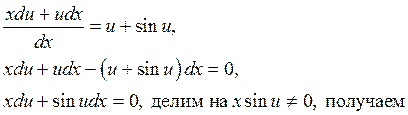
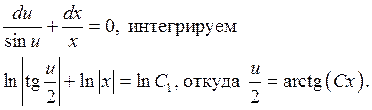
Производя обратную замену, находим общее решение данного уравнения

Используя заданное начальное условие, получим:

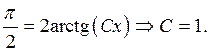
Итак, частное решение имеет вид

Дифференциальные уравнения, приводящиеся к однородным

Уравнение вида

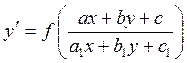
приводится к однородному уравнению с помощью преобразования где определяются системой уравнений

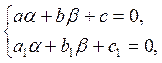
в случае, когда определитель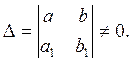

Если же 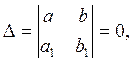то делается следующая замена

Пример 1. Проинтегрировать уравнение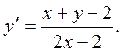

Составляем определитель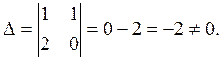

Т.к. определитель то делаем замену

Получаем:

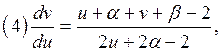
составляем систему уравнений

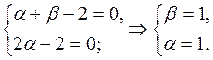
Подставляем найденные значения в (4), получаем:

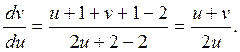
Применим замену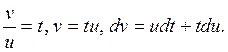

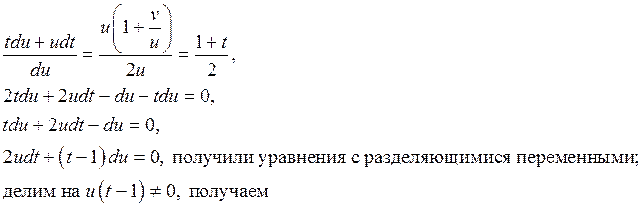
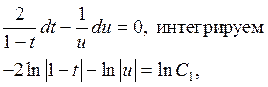
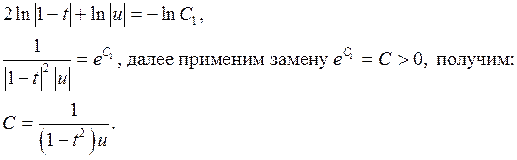
Делая обратную замену переменных, получаем общее решение:

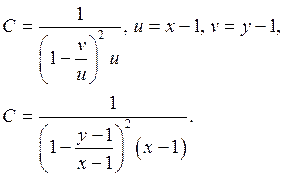
Линейные уравнения. Уравнение Бернулли

Уравнение вида

    (5)

называется линейным дифференциальным уравнением первого порядка.

Решение линейного уравнения ищут в виде произведения двух функций:

Подстановка выражений для и в уравнения (5) приводит его к виду

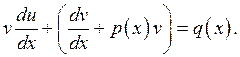
В качестве v выбирают одну из функций, удовлетворяющих уравнению тогда функция и определяется уравнением

Этот метод нахождения решения линейного уравнение называется методом Бернулли.

Для решения уравнения (5) можно также применять метод вариации произвольной постоянной, или метод Лагранжа, состоящий в следующем: сначала находят общее решение соответствующее однородного уравнения (т.е. уравнения, для которого ); величину С, входящую в это  общее решение, полагают функцией х и находят её.

Пример 1. Решить уравнение 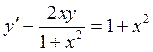при начальных условиях

Это линейное уравнение первого порядка.

Для нахождения общего решения воспользуемся методом Бернулли:

 тогда

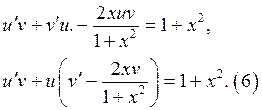
Найдём функцию v из уравнения

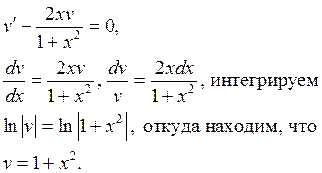
Найденное значение v подставляем в уравнение (6). Учтём также то, что 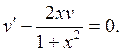 Получаем:

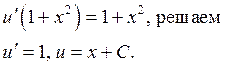
Получаем общее решение

Находим частное решение, исходя из условия

Получаем:

Значит, частное решение имеет вид

Пример 2. Проинтегрировать уравнение  при начальном условии

Это – линейное уравнение. Для его решения применим метод вариации произвольной постоянной, или метод Лагранжа. Решаем соответствующее однородное уравнение.

разделив переменные, получим

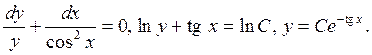
Ищем решение исходного неоднородного уравнения в виде где неизвестная функция. Подставляя в исходное уравнение и

придём к уравнению

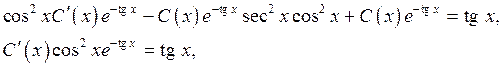
откуда

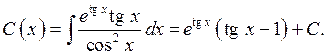
Таким образом, получаем общее решение данного уравнения:

Используя начальное условие получим откуда Следовательно, искомое частное решение имеет вид

Пример 3. Проинтегрировать уравнение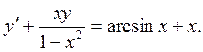

Применим метод вариации произвольной постоянной, или метод Лагранжа.

Интегрируем соответствующее однородное уравнение:

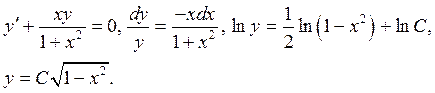
Полагаем теперь тогда

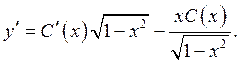
После подстановки в исходное неоднородное уравнение получим

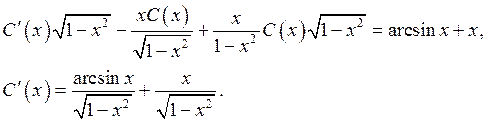
Интегрируя, находим

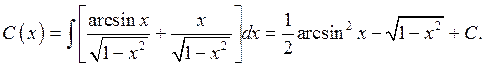
Таким образом, общее решение данного уравнения имеет вид

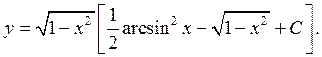
Уравнением Бернулли называется уравнение вида

где a - действительное число. Это уравнение является линейным в случае В других случаях оно сводится к линейному с помощью подстановки

Пример 1. Решить уравнение

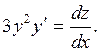Положим тогда После подстановки данное уравнение превратится в линейное:

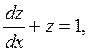общее решение которого

 

Отсюда получаем общий интеграл данного уравнения

Замечание. Уравнение Бернулли можно непосредственно решать методом вариации произвольных постоянный (метод Лагранжа) или методом Бернулли

Пример 2. Решим уравнение примера 1 непосредственно методом Бернулли.

Для облегчения задачи поделим обе части уравнения на получаем:

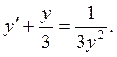
Положим тогда полученное уравнение примет вид

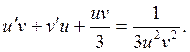Далее

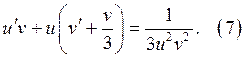
Решаем уравнение 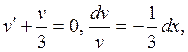интегрируем

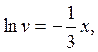откуда находим, что

Найденное значение v подставляем в уравнение (7), получаем:

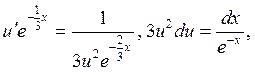интегрируем

откуда выражаем

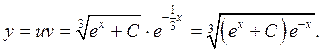
Получаем общее решение

Пример 3. Проинтегрировать уравнение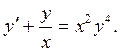

Это – уравнение Бернулли. Проинтегрируем его методом вариации произвольной постоянной (методом Лагранжа). Для этого интегрируем сначала соответствующее линейное однородное уравнение 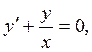решение которого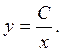

Ищем решение исходного уравнения Бернулли, полагая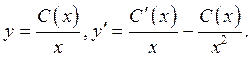Подстановка y и в исходное уравнение даёт

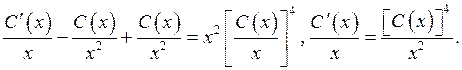
Интегрируем полученное уравнение:

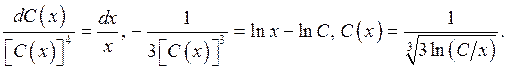
Таким образом, общее решение исходного уравнения

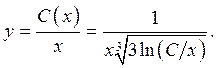
Пример 4. Решить уравнение .

Запишем данное уравнение в виде

.

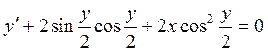Деля обе части уравнения на 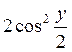, получаем

.

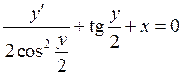Замена 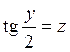,  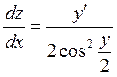приводит это уравнение к линейному

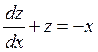, общее решение которого

.

Заменяя  его выражением через , получаем общий интеграл данного уравнения

.  

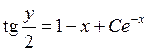Уравнения в полных дифференциалах.

Интегрирующий множитель

Уравнение вида

 (8)

называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции т.е.

В этом случае дифференциальное уравнение (8) можно записать в виде