Использование динамического программирования при решении технологических задач

9 Использование динамического программирования при решении технологических задач

9.1 Функциональные уравнения Беллмана

Пусть некоторый управляемый процесс находится в первоначальном состоянии , которое характеризуется вектором . Множество всех первоначальных состояний определяет .  С течением времени процесс меняется и переходит в конечное состояние . Множество всех конечных состояний –  . Процесс перехода из состояния   в  распадается на N этапов. Причем если процесс находится на i-м этапе в состоянии , то состояние его  на следующем (i+1)-м этапе определяется не только вектором состояний , но и решением , которое принято на i-м этапе. Исходя из этого, вектор состояний следующего этапа можно представить как .  Решение же на каждом  этапе выбирается из множества  возможных решений и определяет значение целевой функции . Целевую функцию  представим в виде суммы функций , значения которых получаются на каждом этапе при переходе из состояния  в состояние  :

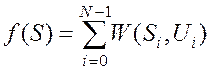.                                                    (9.1)

Тогда задача динамического программирования состоит в том, чтобы из множества возможных решений найти такое решение , которое позволит перевести процесс из первоначального состояния  в конечное состояние  так, что целевая функция (9.1) будет принимать экстремальное значение  при выполнении условий ; ;   (i= 1, …, N-1).

При решении задача динамического программирования разбивается на ряд более простых задач (естественным образом или искусственно). На каждом этапе решается одна из этих задач, причем выбор оптимального решения производиться с учетом будущего, т.е., оптимизируя процесс на каждом этапе, нельзя забывать о всех последующих этапах.

Последний  этап (N=1)-й не зависит от будущего, поэтому на данном этапе выбирают решение, позволяющее получить экстремальное значение целевой функции . Чтобы найти оптимальное решение на N-м этапе, необходимо знать состояние системы на (N-1)-м этапе. Так как состояние процесса на (N-1)-м этапе неизвестно, делают различные предположения о возможных состояниях процесса  на этом этапе, и для каждого предположения выбирают оптимальное решение  на N-м этапе. Таким образом, оптимальное решение на N-м этапе найдено. Затем, учитывая уже полученное оптимальное решение на этапе, получают оптимальное решение на (N-1)-м этапе и т.д. В результате приходят к первоначальному состоянию  процесса.

Для первого этапа предположений о возможных состояниях процесса не делают, так как, состояние  известно. Оптимальное решение первого этапа находят исходя из полученного оптимального решения на втором этапе. Оптимальное решение для всего процесса определяют, просматривая полученные оптимальные решения на всех этапах (от  до ).

Основным методом решения задач динамического программирования является метод функциональных уравнений Беллмана [7].  Для каждой конкретной задачи динамического программирования функциональное уравнение имеет свой вид, характеризующийся видом функции W и величинами S, U. Функциональное уравнение задачи динамического программирования можно записать и в общем виде. Так как решение задач динамического программирования проводится от конца к началу, функциональное уравнение для последнего этапа (N=1) имеет вид

,            (9.2)

где – экстремальное значение целевой функции за нуль этапов, начиная с конечного состояния . Так как за пределами конечного состояния   процесс не рассматривается, то  .

Функциональное уравнение для N-го этапа запишется так

,                       (9.3)

где  является экстремальным значением критерия (целевой функции) за все N этапов процесса, начиная с состояния   – экстремальное значение критерия за (N-1) этапов, начиная с состояния  – величина критерия, полученная на N-м этапе, начиная с состояния  , в результате принятого решения .

Задача динамического программирования методом функциональных уравнений Беллмана решается в такой последовательности [7]:

·  записывают функциональное уравнение (9.2) для конечного состояния процесса (этапа N=1). Так как , то уравнение будет иметь вид . Рассматривают набор фиксированных состояний  и решений  и отвечающих им значений . Среди решений выбирают такое , которое обеспечивает ;

·  переходят к следующему, предпоследнему этапу (N=2). Функциональное уравнение для данного этапа записывают в виде . Для каждого возможного состояния   находят значение  в зависимости от допустимого решения . Затем сравнивают суммы  (в которых учтены полученные значения   последнего этапа) и определяют экстремальную сумму для каждого состояния  и соответствующее условное оптимальное решение  , т.е. определяют , при котором функция   принимает экстремальное значение. Аналогично переходят к следующим этапам (N=3, N=4  и т.д.) до этапа N=N;

·  записывают функциональное уравнение (9.3) для первого этапа N=N. На данном этапе предположения о возможных состояниях процесса не делают, так как первоначальное состояние известно . Для этого состояния следует определить оптимальное решение с учетом всех полученных условно-оптимальных решений второго этапа;

·  проходят весь процесс в прямом направлении от  до  и определяют оптимальное решение  для всего процесса (всей задачи), которое придает целевой функции  экстремальное значение.

9.2 Решение задачи коммивояжера методом динамического программирования

Решение задачи коммивояжера методом динамического программирования было предложено Беллманом, Хелдом и Кэрпом. Опубликованный ими алгоритм является более общим, чем метод