Z=reij=r(cosj+isinj)- комплексное число.
Действия с компл. числами:
Zn=rneinj; ![]()
Z1Z2=r1r2ei(j1+j2); Z1/Z2=r1/r2ei(j1-j2);
![]()
![]()
![]()
![]()
cos(iZ)=chZ
sin(iZ)=ishZ
ch(iZ)=cosZ
sh(iZ)=iShZ
Z1Z2=eZ2*LnZ1;
Выделение целой и мнимой части:
ez=ex+iy=ex(cosy+i siny)=( ex cosy)+i( ex sin y);
W=LnZ=ln|Z|+i(argZ+2pk);
W=cosZ=>u=cosXchY; v=sinXshY;
W=sinZ=>u=sinXchY; v=cosXshY;
W=chZ=>u=chXcosY; v=shXsinY;
W=shZ=>u=shXcosY; v=chXsinY;
Преобразование к Z:
![]()
![]()
Коши-Риман:
W=f(Z)=u+iv;
![]()
Восстановление аналит. ф-ии по её действ.
или мнимой части:
1. гармоничность?
![]() 2.
2.
3. С(y)+С->(u) или C(x)+С->(v)
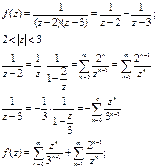 4.f(z) = …
4.f(z) = …
Аналитические функции в точке- дифф в
точке и ее окрестности.
Гармоническая функция - если ее действ.
и мнимая части удв. ур. Лапласа:
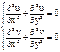 Если для ф-ций это вып-ся,
Если для ф-ций это вып-ся,
то они могут служить
действительной и мнимой
частью нек. гармонической
ф-ции.
Интегральная теорема Коши:
Для односвязной области:
Для многосвязной области:
Интегральная формула Коши:
![]()
![]()
![]()
Qn(x) не имеет действительных корней!!!
Лемма Жордана:
![]()
![]()
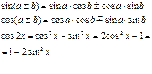
|
УОТ |
ПП |
Пk |
СОТ |
|
|
Rez f(z) |
0 |
1. lim(f(z)(z-z0)) z®z0 2.j( z0)/y’(z0) |
lim(f(z)(z-z0)k)(k-1)/(k-1)! |
С-1 |
|
УОТ |
|
|
Полюс |
|
|
СОТ |
|
A/(x-a) или A/(x-a)k или Mx+N/(x2+px+q)
![]()
Г(1) = 1; Г(р+1) = рГ(р); Г(n+1) = n!
![]()
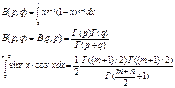
Обратное преобр. Лапласа:
![]()
Пример: (чётная – косинусы, нечётная - синусы)
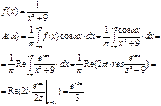
Пример: (Г и В функции)
![]()
Пример: (теорема Руше)
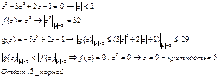
Пример: (в ряд Лорана)
Интегрирование по параметру:
![]()
![]()
![]()
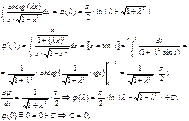
![]()
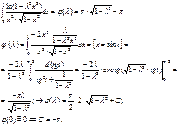
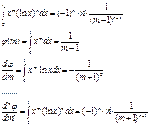
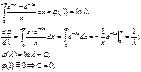
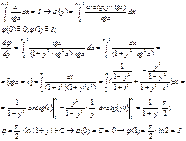
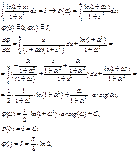
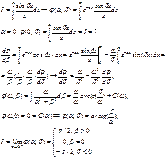
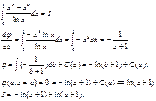
Линии второго порядка:
1. Гипербола
2. Парабола
![]()
3. Эллипс
4. Общее уравнение
![]()
Уравнение (11.14) всегда определяет: либо окружность (при А = С), либо эллипс (при А•С > 0), либо гиперболу (при А•С < 0), либо параболу (при А•С = 0). При этом возможны случаи вырождения: для эллипса (окружности) — в точку или мнимый эллипс (окружность), для гиперболы — в пару пересекающихся прямых, для параболы — в пару параллельных прямых.
1. Комплексный числа и действия над ними, тригономнтричекая и показательная форма компл. числа, корни n-ой степени из компл. числа (1).
2. Определение регулярной (аналитической) функции (5). Условия Коши-Римана. (6)
3.Линейная функция. Её регулярность (аналитичность). Отображение, которое она осуществляет. (1)
4. Степенная функция. Её регулярность (аналитичность). Область однолистности. Отображение, которое она осуществляет. (1-2)
5.Показательная функция. Её регулярность (аналитичность). Область однолистности. Период. Отображение, которое она осуществляет. (1-2)
6.Тригонометрические и гиперболические функции. Их регулярность (аналитичность). Периоды. (3)
7. Логарифм комплексного переменного. Регулярность (аналитичность). Многозначность отображения, которое он осуществляет. (4)
8. Общая степенная функция комплексного переменного. Регулярность (аналитичность). Многозначность отображения, которое он осуществляет.
9. Гармонические функция. Их связь с регулярными функциями комплексного переменного. (7)
10. Геометрический смысл модуля и аргумента производной регулярной (аналитической) функции. Понятие конформного отображения. (8)
11. Определение интеграла от функции комплексного переменного, его связь с криволинейными интегралами. Основные свойства. (9)
12. Интеграл от регулярной (аналитической) функции, Его независимость от пути интегрирования. Формула Ньютона-Лейбница. (12)
13. Интегральная теорема Коши для односвязной и многосвязной областей. (11)
14. Интегральная формула Коши для регулярной (аналитической) функции. (*)
15. Бесконечная дифференцируемость аналитических функций. Интегральная формула Коши для производных регулярной (аналитической) функции. (*)
16. Разложение регулярной (аналитической) функции в ряд Тейлора. Область сходимости. Формулы для коэффициентов. (13)
17. Разложение функции, аналитической в кольце, в ряд Лорана. Формулы для коэффициентов. (14-15)
18. Изолированные особые точки регулярной (аналитической) функции и их классификация. Примеры. (16)
19. Устранимая особая точка. Ряд Лорана и поведение функции в окрестности этой точки. (17)
20. Полюс n-го порядка. Ряд Лорана и поведение функции в окрестности этой точки. (18)
21. Существенно особая точка. Ряд Лорана и поведение функции в окрестности этой точки. (20)
22. Нуля аналитической функции. Порядок нуля. Связь между нулем и полюсом. (19)
23. Вычет аналитической функции в точке. Его связь с рядом Лорана. Основная теорема о вычетах. (21)
24. Формулы для вычисления вычетов в простом и кратном полюсе. (21 и 22)
25. Стереографическая проекция. Бесконечно удаленная точка. Ряд Лорана в окрестности бесконечности. Классификация особенностей в бесконечности. (24)
26. Вычет в бесконечно удаленной точке. Его связь с рядом Лорана. Вторая теорема о вычетах. (24)
27. Приложение теории вычетов к вычислению интегралов по вещественной прямой от рациональных функций. (25)
28. Лемма Жордана. Вычисление несобственных интегралов вида (26)
![]()
29. Логарифмический вычет. Связь числа нулей и полюсов функции внутри замкнутого контура с интегралом по этому контуру. (29)
30. Принцип аргумента. Теорема Руше. (31)
31. Интегралы, зависящие от параметра. Непрерывность по параметру. (31)
32. Интегралы, зависящие от параметра. Интегрирование и дифференцирование по параметру. (32)
33. Несобственные интегралы, зависящие от параметра. Определение равномерной сходимости. Признаки равномерной сходимости. (33)
34. Равномерная непрерывность несобственного интеграла по параметру. Примеры. (34)
35. Интегрирование несобственного интеграла по параметру. Примеры. (34)
36. Дифференцирование несобственного интеграла по параметру. Примеры. (34)
37. Гамма-функция и её свойства: формула понижения, связь с факториалом, формула дополнения. (35-36)
38. Аналитическое продолжение гамма-функции в комплексной плоскости. Её значения на отрицательной полуоси. Свойства Г(z). (35-36)
39. Бета-функция. Её связь с гамма-функцией. Применение к вычислению интегралов. Пример. (36-37)
40. Определение преобразования Лапласа. Его аналитичность. (39-40)
41. Определение преобразования Лапласа. Его обращения с помощью вычетов. (39-40)
42. Степенные ряды. Теорема Абеля.
43. Радиус и круг сходимости степенного ряда. Вычисление радиуса сходимости.
44. Свойства степенных рядов. Сформулировать условия непрерывности, дифференцируемости, интегрируемости степенного ряда в заданной области.
45. Преобразование Фурье и его свойства. (38)
46. Тригонометрические ряды Фурье: вещественная и комплексная формы записи, ряды Фурье для четных и нечетных функций, разложение функций на полупериоде в ряды по синусам и по косинусам.
47. Тригонометрические ряды Фурье: признаки сходимости и равномерной сходимости, теорема единственности.
49. Свойства коэффициентов ряда Фурье.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.