Геометрия и алгебра
1. Каноническое уравнение эллипса – это уравнение
A) ![]()
B)![]()
C)![]()
D) ![]()
2. Каноническое уравнение гиперболы – это уравнение
A) ![]()
B)![]()
C)![]()
D) y2 = 2px
3. Каноническое уравнение параболы – это уравнение
A) ![]()
B)![]()
C) y2 = 2px
D) y2 = 0
4. Окружность – это частный случай
A) параболы
B) гиперболы
C) эллипса
5.
Линия второго порядка Ax2+2Bxy+Cy2+2Dx+ ![]() тогда и только тогда имеет
единственный
тогда и только тогда имеет
единственный
A) ![]()
6. Следующие линии второго порядка являются центральными
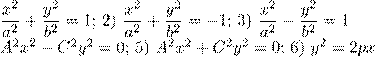 1)
1)
4);
7) y2 − a2 = 0; 8) y2 + a2 = 0; 9) y2 = 0.
Ответ:
A) 1,2,3
B) 1,2,4
C) 1,2; 3,4,8
7. Следующие линии второго порядка не являются центральными
A) 1,3,5,7,9
B) 2,4,6,8
C) 1,2,7,8
D) 5,6,7,8,9
8.
![]() является
является
A) уравнением эллипса
B) уравнением эллиптического цилиндра
C) вплоскости XOY определяетэллипс, впространстве — эллиптический цилиндр
9.Уравнение y2 = 2px определяет
A) эллипс
1
B) параболу
C) на плоскости XOY — параболу, в пространстве — параболический цилиндр
10. Каноническое уравнение гиперболического параболоида – это уравнение
A) ![]()
B)![]()
C) ![]()
11. Множествовсехматрицвида m×n сэлементами из поля P относительно матричного сложения образует:
A) кольцо
B) абелеву группу
C) поле
D) линейное пространство
12. Рангом матрицы называется
A) число ее строк
B) число ее столбцов
C) наивысший порядок отличных от нуля миноров
13. Умножение A · B матриц определено
A) только для квадратных матриц одинакового порядка
B) для любых матриц
C) для матриц A и B таких, что число столбцов матрицы A равно числу строк матрицы B
D) для матриц A и B таких, что число строк матрицы A равно числу столбцов матрицы B
14. Единичная матрица это – A) любая матрица, у которой все элементы равны 1
B) любаяквадратнаяматрица, укоторойвсеэлементы равны 1.
C) любая квадратная матрица, у которой элементы главной диагонали равны 1, а остальные равны 0.
15. Обратная матрица существует
A) для любой матрицы
B) для любой невырожденной матрицы
C) для любой квадратной матрицы
16. теорема Кронекера-Капелли утверждает, что
A) всякая система линейных уравнений совместна
B) существуют совместные системы линейных уравнений
C) система линейных уравнений совместна, если ранг матрицы системы равен числу неизвестных
D) система линецных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы
17. Фундаментальная система решений однородной системы линейных уравнений, это A) множество всех ее решений
B) множество не нулевых решений системы
C) базис подпространства решений
D) базис линейной оболочки, натянутой на строки матрицы системы
18. Есливопределителипоменятьместамидвестроки, то
A) его значение не изменится
B) щнак перед ним изменится на противоположный
C) его значение станет раным 0
19. Множествовсехневырожденныхматрицодногои того же порядка относительно матричного умножения образует:
A) кольцо B) поле
C) абелеву группу
D) группу
20. Множество всех квадратных матриц одного и того же порядка относительно операторов сложения и умножения образует
A) группу
B) поле
C) кольцо
21. Две матрицы одинаковых размеров
A) всегда эквивалентны
B) эквивалентны, если они квадратные
C) эквивалентны, если и только если их ранг совпадает
22. Матрицы A и B
A) если эквивалентны, то подобны
B) если подобны, то эквивалентны
23. Квадратичной формой от переменных x1,x2,...,xn называется
A) оценка квадратов этих переменных
B) всякий однородный многочлен второй степени от этих переменных
24. Матрицей квадратичной формы может быть
A) любая матрица
B) любая квадратная матрица
C) любая симметричная матрица
D) любая невырожденная матрица
25. Закон инерции квадратичныхформ утверждает, что
A) каждую квадратичную форму можно привести к каноническому виду
B) в каноническом виде число членов с положительными коэффициентами равно числу членов с отрицательными коэффициентами
C) если квадратичная форма приведена к каноническомувидуспомощьюдвухлинейныхпреобразований, то число положительных коэффициентов при квадратахновыхпеременных, такжекакичислоотрицательных, в обоих случаях будет одним и тем же
26. Матрица называется ортогональной, если
A) Она квадратная невырожденная
B) если A−1 = AT
C) если A = AT
27. Матрица называется симметричной, если
A) если A = AT
B) если A−1 = AT
C) det A 6= 0
28. Критерий Сильвестра утверждает, что квадратичнаяформаположительноопределенатогдаитолько тогда, когда
A) ее матрица невырождена
B) определитель ее матрицы положителен
C) все главные миноры ее матрицы положительны
2
29. Определитель произведения двух невырожденных квадратных матриц одинакового порядка
A) всегда равен 0
B) иногда равен 0
C) отличен от 0
30. Системасобственныхвекторов, соотвествующих попарно различным собственным значениям
A) всегда линейно независима
B) всегда линейно зависима
C) иногда линейно зависима 31. Какое утверждение верно:
A) всякий линейный оператор, действующий в любомлинейномподпространстве, имеетпокрайнеймере один собственный вектор
B) всякий линейный оператор, действующий в комплексномлинейномпространстве, имеетпокрайнеймере один собственный вектор
32. Матрица преобразования координат пр переходе от одного базиса к другому
A) всегда вырождена
B) всегда невырождена
C) иногда вырождена
33. Какое из этих утверждений верно:
A) поле действительных чисел алгебраически замкнуто
B) поле рациональных чисел алгебраически замкнуто
C) поле комплексных чисел алгебраически замкнуто
34. Пусть A — матрица, имеющая n строки m столбцов, n > m. Тогда
A) ранг пространства векторов-столбцов меньше ранга пространства векторов-строк
B) ранг пространства веторов-столбцов больше ранга пространства векторов-строк
C) эти ранги равны
35. Любая ортогональная система ненулевых векторов евклидова подпространства
A) линейно зависима
B) иногда линейно зависима
C) всегда линейно независима
36. Множество линейных операторов, действующих в линейном пространстве X относительно операций сложения и умножения всегда являются
A) полем
B) кольцом
37. При умножении линейных операторов их матрицы
A) перемножаются
B) складываются
38. Верно ли, что всякаяквадратнаяматрица подобна треугольной
A) да
B) нет
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.