Дифференциальные уравнения
1. Какое уравнение с неизвестной функцией называетсяобыкновеннымдифференциальнымуравнением?
A) уравнение, которое содержит производные от искомой функции и может содержать искомую функцию и независимую переменную.
B) уравнение, котороесодержитнескольконезависмыхпеременных, искомуюфункциюичастные производныеотискомойфункциипонезависимым переменным
C) всякое уравнение, содержащее искомую функцию под знаком интеграла.
2.
A)
B)
C)
D)
3. Можно ли по аналитическому виду правой части уравнения и по начальным данным сделать заключениеосуществованиииединственностирешения?
A) да
B) нет
4. Метод последовательных приближений (метод Пекара) решения задачи Коши является
A) точным аналитическим методом
B) приближенным аналитическим методом
C) численным методом
5. Методпоследовательныхприближенийрешенияуравнения y0 = f (x,y) приусловии y (x0) = y0 состоит в том, что
A)
ИскомоерешениепредставляетсярядомТейлора коэффициенты которого можно
получить последовательным дифференцированием данного уравнения 
и так далее.
B) Искомое решение y (x) получают как предел последовательности функций yn (x), которые находятся по итерационной формуле yn (x) = y0 +
6. Какое решение называется особым?
A) решение, полученноеврезультатеподстановки начальных условий в общее решение
B) решение y = y (x), в каждой точке которого нарушается единственность решения задачи Коши
C) решение, которое может быть получено из формулы общего решения при конкретном числовом значении произвольной постоянной C
7. Функция
y 0, y > 0 является:
A) линейной
B) однородный
C) неоднородный
8. Уравнение
решается:
A) подстановкой y = u(x) · v (x)
B) подстановкой y = u(x) · x
C) подстановкой y0 = p(x)
9. Каким методом интегрируется линейное неоднородное уравнение?
A) методом Бернулли.
B) методом Лагранжа
C) методом неопределенных коэффициентов
D) методом Лагранжа и Бернулли
E) методамиБернулли, Лагранжа, неопределенных коэффициентов.
10. КакинтегрируетсяуравнениеБернулли y0+ p(x)y = g (x)ym?
A) методом Лагранжа
B) методом Бернулли
C) подстановкой z = y1−m
D) любым из указанных методов
11. При каком условии уравнение M (x,y)dx + N (x,y)dy = 0 являетсяуравнениемвполныхдифференциалах?
A) M (x,y) = −N (x,y);
B) 
;
C) 
;
D) R Mdy = R Ndx.
12. Какой вид имеет уравнение Клеро?
A) y = ϕ(y0) x + ψ (y0)
B) y = xy0 + ψ (y0)
C) y0 + ϕ(x)y = ψ (y)
13. Как находится общее решение уравнения Клеро?
A) введением параметра p(y0 = p)
B) заменой в уравнении y0 на C
C) заменойискомойфункции, положив y0 = z (y)
D) введение параметра p или заменой в уравнении y0 на C
14. Как понижается порядок уравнения, не содержащего искомой функции?
A) введением новой искомой функции p = p(x), полагая y(k) = p
B) введением новой искомой функции p = p(x), полагая y0 = p
C) введением новой искомой функции p = p(y), полагая y0 = p
15. Как понижается порядок уравнения, не содержащего независимой переменной?
A) подстановкой y(k) = p(x)
B) подстановкой y0 = p(x)
C) подстановкой y0 = p(y)
16. Какой вид имеет неоднородное линейное уравнение n-го порядка?
A) y(n) = f (x)
B) y(n) +p1 (x)y(n−1) +...+pn−1 (x)y0 +pn (x)y = f (x)
C) L[y] = 0
17. Определитель Вронского имеет вид:
A)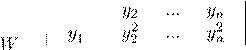
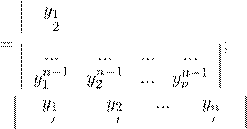
B)
C)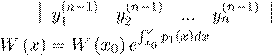
18. Как при помощи определителя Вронского узнать, образуют ли данные n решений однородноголинейногоуравнения n-гопорядкафундаментальную систему решений?
A) W (x) = 0;
B) W (x) 6= 0;
C) W (x0) = 0, x0 ∈ (a,b)
19. Как строится общее решение однородного линейного уравнения n-го порядка по фундаментальной системе решений?
n
A) y = P Ckyk, Ck−const, y1,y2,...,yk — фун-
k=1
даментальная система решенийуравнения L(y) =
0 n
B) y = P Ckyk0 k=1
C)
20. Общее решение неоднородного уравнения L[y] = f (x) с непрерывными коэффициентами pi (x) имеет вид:
A) y = y0 + Y
B) y = y0 − Y
C)
,
где y0 общее решение
соотвествующегооднородногоуравнения, Y
– частноерешение данного уравнения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
