Дифференциальные уравнения. Уравнение с неизвестной функцией. Метод последовательных приближений (метод Пекара) решения задачи Коши, страница 2

21.  Если известно фундаментальная система решений y₁,y₂ однородного уравнения L[y] = 0, то общее решение соотвествующего неоднородного уравнения L[y] = f (x) может быть найдено по формуле y = C₁ (x)y₁ + C₂ (x)y₂, где функция C_i (x), i = 1,2 опеределяется из системы уравнений

(

C₁ (x)y₁ + C₂ (x)y₂ = 0;

A)

= 0;

(

= 0;

B)

 = 0;

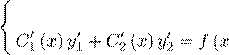
= 0; C)

);

22. Линейноедифференциальноеуравнениевторого порядка имеет вид L[y] = 0. Если корни k₁ и k₂ характеристическогоуравнениядействительны и различны, то общее решение уравнения записывается в виде:

A)  y = e^k1x (C₁ + C₂x)

B)  y = C1ek1x + C2ek2x

C)  y = e^αx (C₁ cosβx + C₂ sinβx)

23. Линейноедифференциальноеуравнениевторого порядка имеет вид L[y] = 0. Если корни k₁ и k₂ характеристическогоуравнениядействительны иравны, ообщеерешениеуравнениязаписывается в виде:

A)  y = e^k1x (C₁ + C₂x)

B)  y = C1ek1x + C2ek2x

C)  y = e^αx (C₁ cosβx + C₂ sinβx)

24. Линейноедифференциальноеуравнениевторого порядка имеет вид L[y] = 0. Если корни k₁ и k₂ характеристического уравнения комплексные числа, ообщеерешениеуравнениязаписываетсяв виде:

A)  y = e^k1x (C₁ + C₂x)

B)  y = C1ek1x + C2ek2x

C)  y = e^αx (C₁ cosβx + C₂ sinβx)

25. Укажите вид частного решения уравнения y⁰⁰ + y = 2sinx. A) y = Acosx + B sinx e

B)  y = Axsinx e

C)  y = x(Acosx + B sinx) e

26. Укажите вид частного решения уравнения y⁰⁰ − 2y⁰ + y = xe^x. A) y = e^x (Ax + B) e

B)  y = xe^x (Ax + B) e

C)  y = x²e^x (Ax + B) e

27. Укажите вид частного решения уравнения y⁰⁰ − 4y⁰ + 4y = sin2x + e^2x. A) y = Asin2x + Bxe^2x e

B)  y = Acos2x + B sin2x + Cx²e^2x e

C)  y = Acos2x + B sin2x + Cx³e^2x e

28. Уравнение решается:

A)  методом неопределенных коэффициентов

B)  последовательным интегрированием

C)  методомвариациипроизвольныхпостоянных

29. Решение однородного уравнения Эйлера можно искать в виде:

A)  y⁰ = p(x)

B)  y = x^k C) y = lnx

30. Решение неоднородного уравнения Эйлера можно искать в виде:

A)  y = x^k

B)  y = e^t

C)  y = lnx

31. Уравнение Бесселя имеет вид:

A)  x²y⁰⁰ + xy⁰ + ky = 0

B)  C)

32. Какая из приведенных систем записана в нормальном виде:

A)

1,2,...n n

B)  y_i⁰ = ^P a_ik (x)y_k + f_i (x), i = 1,2,...,n

k=1

C)  y⁰ = A(x)y + f (x)

33. Какое из соотношений называется тождеством Якоби:

^Rxx0 p¹(x)dx

A)  W (x) = W (x₀)e

B)  и что из него следует?

34. Методисключениярешениянормальныхсистем уравнений n-го порядка состоит:

A)  в приведении системы к одному уравнению n-го порядка

B)  в составлении характеристического уравнения

C)  в приведении системы к симметрической форме

35. Данные n решенийоднороднойлинейнойсистемы n уравнений образуют фундаментальную систему решений, если определитель Вронского:

A)  W (x) = 0

B)  W (x) > 0

C)  W (x) 6= 0

D)  W (x) < 0

36. Всегда ли методом исключения можно привести нормальную систему n уравнений к одному уравнению n-гопорядкасоднойнеизвестнойфункцией?

A)  да

B)  нет

37. Линейная однородная система с постоянными коэффициентами всегда интегрируется в элементарных функциях. Это можно показать, используя метод

A)  исключения

B)  метод интегрируемых комбинаций

C)  метод Эйлера

D)  матричный метод

38. Решение уравнения Бесселя можно получить

A)  методомпоследовательногодифференцирования

B)  методом неопределенных коэффициентов, используя разложения решения в степенной ряд

C)  методом неопределенных коэффициентов, используя разложение решения в обобщенный степенной ряд

39. метод последовательного приближения решения задачи Коши y⁰ = f (x,y), y (x₀) = y₀ сводится

A)  к сведению задачи к эквивалентоному интегральному уравнению

B)  к сведению задачи к эквивалентоному интегральному уравнению и применению к последнему метода последовательных приближений

40. Число произвольных постоянных, входящих в общее решение нормальной системы равно A) число неизвестных функций плюс 1

B)  число неизвестных функций

C)  число неизвестных функций минус 1

41. Если число α + iβ является корнем кратности k (k ≥ 1) характеристического уравнения соотвествующего однородного уравнения, то частное решение неоднородного уравнения имеется в виде: A) y (x) = xe^αx [P (x)cosβx + Q(x)sinβx] e

B) y (x) = x^k−1e^αx [P (x)cosβx + Q(x)sinβx]

C)