, доцент кафедры физики РГУ им. (продолжение 2)
ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ
В классической механике был известен принцип относительности Галилея, согласно которому во всех ИСО все законы механики имеют один и тот же вид, или, иначе говоря, законы механики инвариантны относительно преобразований координат Галилея. (Инвариант – invariant - неизменяющийся).
Найдем связь между координатами точки М в двух различных ИСО – К и К¢.
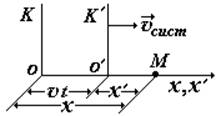 В начальный момент т.т. О и О¢ совпадают(см.рис.). Затем система К¢¢
начинает двигаться с постоянной скоростью vсист относительно
системы К вдоль оси х. Из рисунка видно, что координаты точки М
связаны между собой уравнением: х = х¢
+ vсист×t. Продифференцируем это уравнение по
времени и получим связь между скоростями: v = v¢ + v сист .
Дифференцируя еще раз, найдем соотношение между ускорениями: а = а¢ . Обобщая на случай трехмерного
движения, запишем в векторной форме.
В начальный момент т.т. О и О¢ совпадают(см.рис.). Затем система К¢¢
начинает двигаться с постоянной скоростью vсист относительно
системы К вдоль оси х. Из рисунка видно, что координаты точки М
связаны между собой уравнением: х = х¢
+ vсист×t. Продифференцируем это уравнение по
времени и получим связь между скоростями: v = v¢ + v сист .
Дифференцируя еще раз, найдем соотношение между ускорениями: а = а¢ . Обобщая на случай трехмерного
движения, запишем в векторной форме.
|
|
Эта формула называется преобразованиями координат
Галилея. |
|
|
формула сложения скоростей в классической механике.
|
|
|
ускорения точки М одинаковы в К и К¢,умножив ускорения на массу точки m, запишем 2-й закон Ньютона, и приходим к выводу, что для данной точки М в любой ИСО ускорения одинаковы, закон движения – одинаков, силы – одинаковы. |
В классической галилеево-ньютоновской механике предполагалось:
|
|
|
длина отрезка, определяемая как разность координат его
начала и конца, в любой ИСО одинакова |
|
|
течение времени и длительность промежутка времени одинаковы в любой ИСО |
|
Принцип относительности Галилея можно сформулировать еще и так: никакими механическими опытами невозможно установить покоится данная ИСО или движется равномерно и прямолинейно, т.е. все ИСО равноправны, а покой и равномерное прямолинейное движение неразличимы. Например, мы находимся в каюте корабля, иллюминатор занавешен, и мы хотим узнать, движется корабль или он неподвижен. Пытаемся провести какие-либо механические опыты: подбрасываем мяч, смотрим на качающийся маятник и пр. Никакие механические опыты не помогут нам ответить на вопрос: корабль движется равномерно и прямолинейно или покоится.
СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (СТО)
Специальная теория относительности (СТО) или релятивистская механика - это новая физическая теория, созданная Эйнштейном в 1905 г. и пришедшая на смену классической ньютоновской механике. Заслуга Эйнштейна не только в том, что он открыл новые формулы, но главным образом в том, что он радикально изменил наши представления о пространстве и времени. В СТО рассматривается движение тел в инерциальных системах отсчета (ИСО) со скоростями, близкими к скорости света.
В конце 19 века Максвелл создал электромагнитную теорию, которая обобщила все известные к тому времени электрические и магнитные явления. Эта теория имела значимость не менее важную, чем ньютоновская механика. Но оказалось, что уравнения Максвелла в разных ИСО имеют различный вид. Возникшие затруднения можно было устранить, если предположить, что:
1) уравнения Максвелла неправильны (но они подтверждаются опытами),
2) принцип относительности Галилея неверен, 3) и уравнения Максвелла и принцип относительности Галилея верны, но неверны формулы преобразования координат. Именно третье решение оказалось верным. Новые выражения для преобразования координат и времени называются преобразованиями Лоренца. При использовании этих преобразований уравнения Максвелла становятся инвариантными, но основной закон классической механики ma = F – нет (см. дальше – «Релятивистская динамика»).
В основе СТО лежат два постулата, выдвинутые Эйнштейном:
|
1) Во всех ИСО все законы природы имеют одинаковую математическую форму при использовании преобразований координат и времени Лоренца или, иначе, все законы природы инвариантны относительно преобразований Лоренца. |
Этот постулат называют принципом относительности в том смысле, что не существует какой-либо одной, преимущественной системы отсчета, все ИСО равноправны. Но если принцип относительности Галилея касался только законов механики, то принцип относительности Эйнштейна – всех законов природы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.