Марковская модель защиты информации при заданных ограничениях. Уровни защищенности информации при использовании различных моделей, страница 6

5.3 Система защиты имеет шесть каналов воздействия, три из которых защищены неоднородными средствами защиты, три остались не защищенными (рис. 2.13).

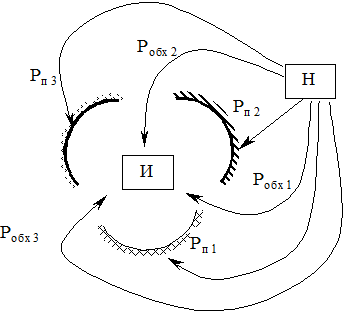
Рисунок 2.13 Модель системы  защиты информации

Тогда по аналогии с 5.1 и 5.2 граф и матрица состояний и переходов примут вид:

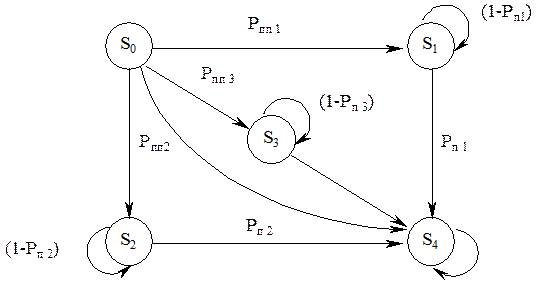
Рисунок  2.14 Граф состояний и переходов

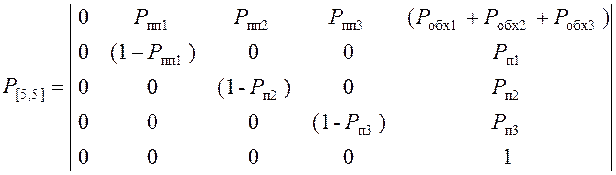
Воспользовавшись методом индукции, представим  граф и матрицу состояний и переходов для общего случая

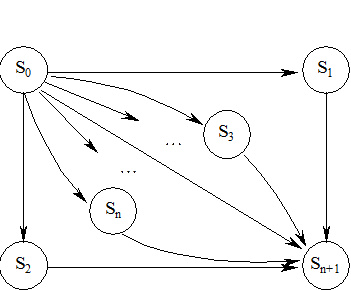
Рисунок 2.15 Граф состояний и переходов

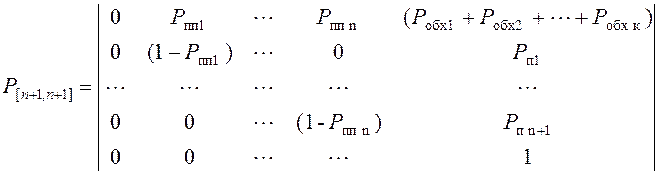      (2.20)

В остальном методика оценки вероятности преодоления остается аналогичной той, что рассмотрена в варианте 3.

Марковские модели являются универсальным инструментом исследования систем. Однако требование к экспоненциальному распределению времени нахождения в том или ином состоянии существенно ограничивает область их корректного применения. Поэтому в данной работе, наряду с моделями вариантов 3,4,5, разработана имитационная модель воздействия нарушителя, представляющая собой численный метод статистического исследования процесса взлома системы защиты информации. Модель построена на сочетании принципов особых состояний и узловых точек  [Бусленко]. Ввиду того, что события, соответствующие взлому ( не взлому) того или иного устройства защиты в данной попытке являются вероятностными, а  процесс взлома реализуется как правило методом подбора или случайного угадывания, в модели используется совокупность случайных чисел с квазиравномерным законом распределения в интервале  [ 0, 1].

Целью имитации является оценка возможных последствий взаимодействия воздействий нарушителя  и системы защиты в условиях, наиболее адекватных исследуемому процессу.

Построение математической модели  включает описание параметров и переменных, их взаимосвязи в общем алгоритме функционирования системы. Модель представлена в виде алгоритмического описания моделируемого процесса.

Адекватность модели исследуемому процессу оценена путем получения следующих утвердительных ответов:

в модели исключены все несущественные переменные, не улучшающие способность предсказания поведения системы;

в модели учтены все необходимые (существенные) входные и управляющие параметры и переменные;

функциональные связи между входными параметрами и выходными переменными отвечают содержательной стороне процесса взлома системы защиты;

оценки случайных параметров построенной модели статистически значимы.

Машинная программа модели реализована на языке С++.

Требуемая статистическая точность результатов обеспечена обоснованием выбора объема эксперимента - числа реализаций исследуемого процесса.

Пусть событие А - факт выполнения системой защиты своей функции. Вероятность свершения события А в процессе статистических испытаний оценивается как  Р ( А ) = m / N , где  m - число случаев наступления события А при N  реализациях. В силу предельной теоремы теории вероятностей частость  m / N  при достаточно большом N  имеет распределение близкое к нормальному, поэтому

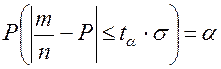                               (2.21)

Точность оценки m / N  определяется по формуле:

, где  a  - доверительная вероятность;

t_a - квантиль нормального закона, соответствующий заданному значению a и определяемый по таблицам нормального распределения    [Вентцель] :

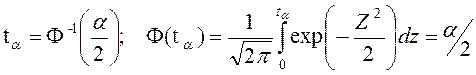                (2.22)

где  -  Ф - функция Лапласа;

Ф^-1 - функция, обратная функции Лапласа;

s² - дисперсия частости m / N , определяемая по формуле:

                                             (2.23)

Преобразуя ( 2.22 ) и ( 2.23 ), получим

                                          (2. 24)

Учитывая, что оцениваемые вероятности имеют малые значения, перейдя в выражении ( 2.23 )  от абсолютной точности  e  к относительной d = e / Р  получим выражение

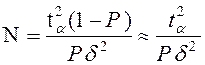                                  (2.25)

Как следует из (2.25 ), для определения объема имитационных экспериментов необходимо знать значение  Р , а оно в данном случае является неизвестным. С учетом этого в работе применен  «последовательный алгоритм уточнения объема выборки» в результате выполнения которого установлено требуемое значение N. С некоторой степенью приближенности данный процесс может считаться стационарным и эргодическим. Из этого сделан вывод о том, что обработка и анализ данных, полученных при моделировании могут осуществляться традиционными  методами математической статистики (усреднением полученных в каждой реализации результатов).