Марковская модель защиты информации при заданных ограничениях. Уровни защищенности информации при использовании различных моделей, страница 5

Для такой модели системы защиты граф состояний и переходов примет вид, изображенный на рис. 2.7 :

Рисунок 2.7- Граф состояний и переходов 

В общем виде матрица переходных вероятностей будет иметь вид:

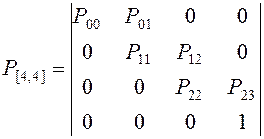                                     (2.17)

Рассчитаем по ( 2.15 ) вероятность взлома системы защиты за        k = 3 попытки.

Пусть     Р₀₁ = 0,7;  Р₁₂  = 0,6;   Р₂₃  = 0,3.  При таких исходных данных получим матрицу (2.17)   

 , а вектор исходного состояния Р_<4>[0] = < 1 0 0 0 >.

Тогда

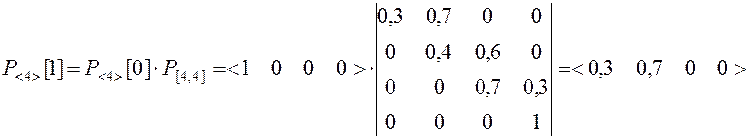
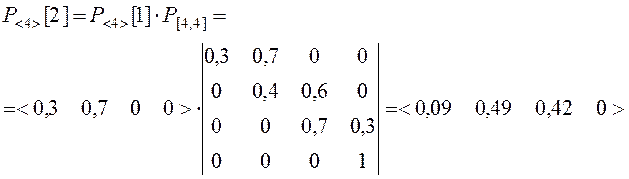
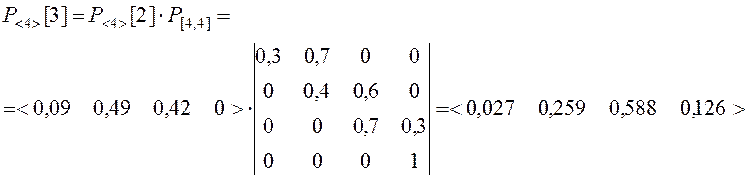
Таким образом, после трех попыток взлома вероятность преодоления системы защиты Р_п⁽³⁾ = 0,126.

Третьей важной особенностью систем защиты информации в современных ИС является   возможность восстановления вскрытых средств защиты либо по времени, либо по действиям администратора. Например, по истечение некоторого наперед заданного интервала времени, меняется имя пользователя, изменяется пароль доступа и т.д.  С учетом этого разработан четвертый вариант модели.

Вариант 4. Процесс вскрытия системы защиты информации в этой модели отличается от предыдущего тем, что нарушитель, при попытке вскрытия очередного средства защиты обнаруживает, что предыдущие эшелоны (эшелон) восстановлены и ему необходимо приступать к взлому защиты, начиная с первого эшелона. Учитывая тот факт, что вероятности вскрытия средства защиты незначительны (например, нарушитель знает  один из миллиона возможных значений пароля), можно считать события воздействий независимыми. Тогда, граф состояний и переходов такого процесса примет вид, изображенный на рис. 2.8.

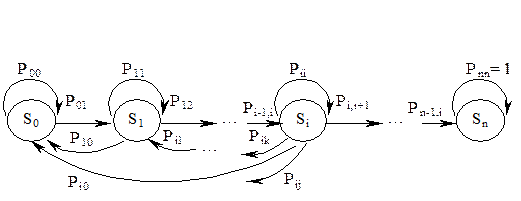
Рисунок 2.8 Граф состояний и переходов

Дальнейшие расчеты проводятся аналогично тем, что приведены для модели 3.

Рассчитаем вероятность взлома системы защиты для графа, представленного на рис. х.6, и вероятностях  Р₀₁ = 0,7;  Р₁₂ = 0,6;          Р₂₃ = 0,3;  Р₁₀ = 0,1;  Р₁₁ = 0,3;  Р₂₀  = Р₂₁ = 0,1;  Р₂₂ = 0,5  при числе попыток взлома  k = 3.

Для модели системы защиты, представленной на рис.2.6 граф состояний и переходов примет вид, изображенный на рис. 2.9.

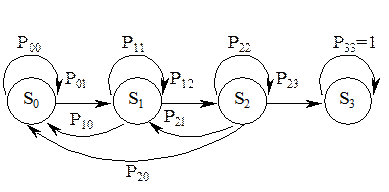
Рисунок 2.8 Граф состояний и переходов

В дальнейшем методика оценивания вероятности взлома системы защиты останется аналогичной  той, что, использована в варианте 3.

 =

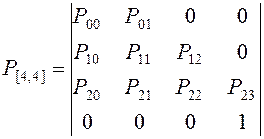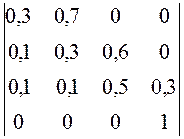
Р_<4>[0] = < 1 0 0 0 >.

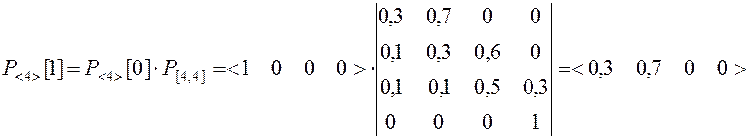
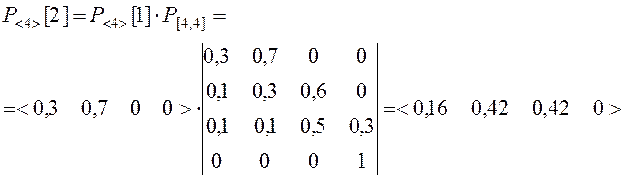
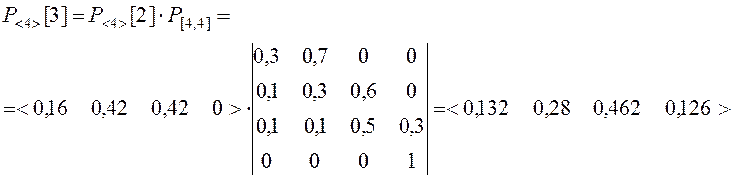
Таким образом, после k=3 попыток воздействия, система защиты (рис.2.6) при исходных данных (2.18) будет преодолена с вероятностью Р_п⁽³⁾=0,126.

Для распределенных ИС ВН, где невозможно построить круговую систему защиты (полностью перекрыть все возможные каналы воздействия), разработана модель пятого варианта в нескольких модификациях.

Вариант 5. Для разработки марковской модели воздействия нарушителя на систему защиты, состоящую из системы очаговых преград, воспользуемся методом индукции.

5.1 Система защиты информации имеет вид, изображенный на рис. 2.10.     

Рисунок 2.10 Модель очаговой системы защиты

Исходные данные, ограничения и допущения:

система защиты имеет три канала воздействия;

два канала защищены неоднородными средствами защиты с вероятностями преодоления с одной попытки - Р_п1 и Р_п2 ;

вероятности попадания на каналы защиты в одной попытке воздействия соответственно равны - Р_пп1 и Р_пп2 , вероятность попадания в данной попытке на незащищенный канал Р_обх ;

при попадании на незащищенный канал нарушитель преодолевает систему защиты с вероятностью, равной  1;

попытки воздействия являются независимыми, преодоленные средства защиты не восстанавливаются.

Формализуем возможные состояния системы при воздействии нарушителя.

S₀ - нарушитель совершает попытку преодоления системы защиты;

S₁ - нарушитель при совершении попытки преодоления системы защиты попал на защищенный канал 1;

S₂ - нарушитель при совершении попытки преодоления системы защиты попал на защищенный канал 2;

S₃ - нарушитель преодолел систему защиты.

Граф и матрица состояний и переходов для такой системы примут вид:

      

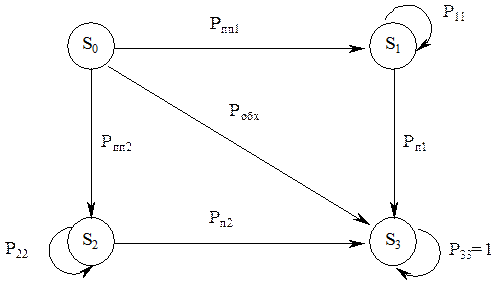
Рисунок 2.11   Граф состояний и переходов

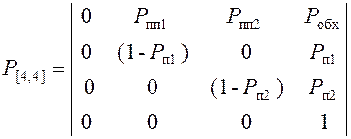                     ( 2.19)

5.2 Граф и матрица  состояний и переходов для модели системы защиты представленной на рис. 2.12 будут иметь аналогичный вид, за исключением того, что элемент матрицы Р₀₃ вычисляется как сумма вероятностей Р₀₃ = Р_обх = Р_обх1 + Р_обх2. Такая запись всегда будет математически корректна, т.к. матрица состояний и переходов является стохастической.

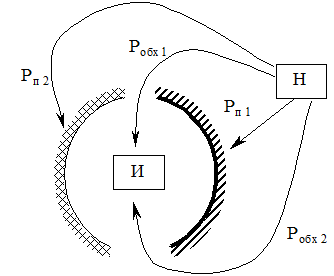
Рисунок 2.12 Модель системы  защиты информации