Марковская модель защиты информации при заданных ограничениях. Уровни защищенности информации при использовании различных моделей, страница 3

В качестве параметров модели выступают:

вероятность преодоления i -го эшелона защиты  с одной попытки -  P⁽¹⁾_{п i}  ;

Число эшелонов защиты   -  m ;

Число попыток воздействия    - k .

В качестве переменной - вероятность не преодоления системы защиты P_{нп m} .

Тогда, если все эшелоны защиты однородны (имеют одинаковую вероятность преодоления - P_{п i} ), а число попыток воздействия равно k, то

P^(k)_{нп m} = ( 1 - (P⁽¹⁾_{п i})^m )^k                                     (2.4)

Отсюда нетрудно решить и обратную задачу. Сколько необходимо иметь эшелонов защиты, чтобы добиться требуемого уровня защищенности  информации при использовании такой модели?  Для этого необходимо лишь проделать следующую последовательность действий:

1.P^(k)_{нп m} = ( 1 - (P⁽¹⁾_п)^m )^k ;

2.                                                                                            (2.5)

3.  

4.  

5.   ;

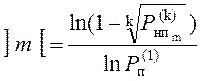Знак    означает операцию округления в сторону увеличения.

Если эшелоны защиты не однородны ( P_п1 ¹ P_п2 ¹ ... ¹ P_{п i} ¹ P_{п m}), то выражение ( 2.4 ) примет вид

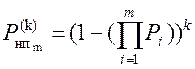.                                         (2. 6)

Известен и другой подход к созданию моделей воздействия нарушителя на систему преград. Он основывается на свойстве «старения» информации. Следствием этой причины является необходимость решения задачи определения времени t_н , после которого информация теряет ценность для тех, кто ее пытается получить.

Решение этой задачи не является сложным, если известны зависимости изменения во времени «стоимости» хранения и «стоимости» получения  информации от времени. Так, если «стоимость»   хранения информации во времени изменяется по линейному закону С_и(t)=k₁t+b,а стоимость преодоления системы защиты  - по пропорциональной зависимости С_п(t)=k₂t, найти время t_н, после которого взлом защиты становится не целесообразным можно как аналитическим, так и графическим путем.

Пусть k₁ = - 0,5 ; b = 10 ; k₂ =  2. Тогда

С_и(t)= С_п(t);

k₁t+b = k₂t ;

k₂t - k₁t = b ;                                                                                            (2.7)

;

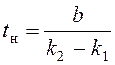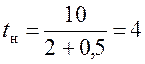 [ ед. времени]

Рисунок 2.3-Графическое решение задачи

Вместе с тем учет «старения» информации приводит к необходимости учета фактора времени и при выборе показателя оценки защищенности, который в данном случае становится главным показателем, т.к. в нем время выступает ограничивающим фактором. В качестве такого показателя будем использовать вероятность не преодоления системы защиты за время, не превышающее заданное  P_нп(t £ t^з) .

Ограничения, используемые в моделях 1и 2 являются очень сильными, и в значительной мере не отражают реального построения систем защиты. В первую очередь это обусловлено особенностями распределенных ИС как объектов использования информации. Одной из таких особенностей ( в том числе и в АСУ) является значительные, разнесенные по территории того или иного региона размеры. Следствием этого является большая трудность, а в ряде случаев не возможность создания замкнутой круговой преграды вокруг всей ИС ВН, и необходимость перехода к очаговой системе преград, имеющей обходные пути (рис 2.4).

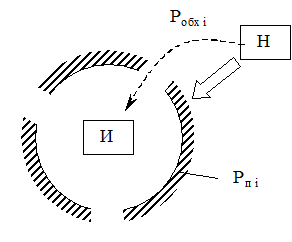
Рисунок 2.4 - Модель очаговой  системы защиты

В [ Мельников ]  предлагается для оценки защищенности информации в такой модели использовать следующие выражения

Р_нп = 1, если t_ж < t_н и Р_обх = 0 ;

Р_нп = ( 1 - Р_п( t £ t_ж) ) ;                                                                  (2.8)

Р_нп = ( 1 - Р_п( t £ t_ж) )(1 - Р_обх),

где  Р_п( t £ t_ж) = 0, если t_ж < t_н ;

Р_п( t £ t_ж) > 0, если t_ж > t_н ;

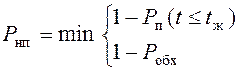
где t_ж - время «жизни» информации.

Если обходных путей несколько, то

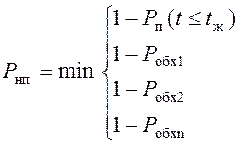
где Р_п( t £ t_ж), например, для взлома системы защиты, основанной только на методе паролирования, рекомендуется находить по выражению

,                                              

где    n   - количество попыток подбора пароля;

А  - число символов  в выбранном алфавите;

S   - длина пароля.    

Эту же задачу на наш взгляд можно решить и следующим способом:

1) вероятность преодоления системы преград с одной попытки

;                      (2.9)

2) вероятность не преодоления с одной попытки

Р⁽¹⁾_{н пр} = 1 - Р⁽¹⁾_пр ;                                                      (2.10)

3) вероятность преодоления с k  попыток

  Р^(к)_пр = 1 - (1 - Р⁽¹⁾_пр)^к ;                                                 (2.11)