Марковская модель защиты информации при заданных ограничениях. Уровни защищенности информации при использовании различных моделей, страница 2

При этом необходимо иметь ввиду следующее. В большой группе задач не удается однозначно предсказать последствия принимаемых решений, поскольку некоторые явления, описываемые параметрами и переменными математической модели, определить точно не представляется возможным. В этом случае принято говорить, что принятие решения осуществляется в условиях неопределенности. При поиске решения в таких задачах выделяют два основных подхода к моделированию. В первом, предполагают, что функциональные связи модели, описывающие существенные свойства моделируемой системы, носят статистический (стохастический или вероятностный) характер. При этом каждому значению одной переменной соответствует не какое-то определенное значение, а множество возможных значений другой переменной, в том числе и множество значений целевой функции. Иначе говоря, каждому значению одной переменной соответствует определенное статистическое распределение другой переменной. Вероятностное распределение переменной (или неопределенного параметра) считается известным. Модели, построенные по такому принципу называются моделями со случайными факторами. При втором подходе к моделированию систем с неопределенностью, считают, что известна лишь область изменения переменной или неопределенного параметра, т.е. исходная информация имеет множественные условия. Особенно это характерно для моделей  противоборствующих (конкурирующих) систем (как для систем защиты), где точно предсказать действия сторон зачастую оказывается невозможным. Модели, построенные на этих условиях называют моделями с неполной информацией.

В настоящее время, несмотря на большое количество проведенных исследований у нас в стране и особенно  за рубежом, единая и общепринятая модель воздействия нарушителя (противника, злоумышленника) на информационные массивы, хранящиеся и обрабатываемые в ИС еще не создана.      Однако, общими усилиями разработан подход к решению этой проблемы, суть которого состоит в разработке общей теории защиты (сохранении) какого-либо предмета от несанкционированного доступа (уничтожения, искажения, похищения, размножения) и приложение ее к ИС с учетом особенностей информации как предмета защиты и самих ИС, как объектов ее использования.

Разработан, опубликован и используется ряд моделей воздействия. С точки зрения используемого математического аппарата в основном все они базируются на логико-вероятностный подход.

Вариант 1.  Простая  вероятностная модель (рис. 2.1).

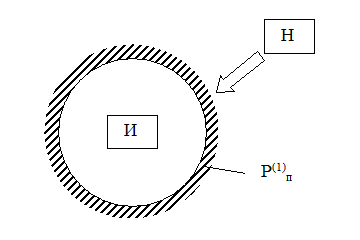
Рисунок 2.1-Простая вероятностная  модель 

Используемые ограничения и допущения:

1) нарушитель пытается завладеть информацией,  хранящейся за некоторой преградой (защитой), совершая ограниченное k число независимых попыток воздействия;

2) преграда (защита) единственная, замкнутая (круговая), однородная и действует постоянно.

3) система защиты после каждой попытки успевает полностью восстановиться.

В качестве параметров модели выступают: вероятность преодоления защиты с одной попытки -  Р⁽¹⁾_п и число попыток  k .

В качестве переменной - вероятность ее не преодоления Р_нп .

Тогда  в соответствии с логико-вероятностным подходом

                                          Р⁽¹⁾_нп = 1 - Р⁽¹⁾_п                                                (2.1)

а вероятность не преодоления системы  защиты с k попыток

Р^(k)_п = 1-(1 - Р⁽¹⁾_п )^k  

                                      Р^(k)_нп = 1 - Р^(k)_п =(Р⁽¹⁾_нп )^k                               (2.2)

Таким образом, совершая  требуемое число попыток  k^Тр , нарушитель может добиться заданной цели даже при высоком уровне защищенности информации.

Пусть требуется вскрыть систему защиты с вероятностью Р_п ³ Р_п^Тр

Тогда

                                                             (2.3)

    

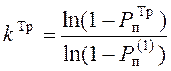
В свою очередь хранитель информации для повышения уровня защищенности может создать несколько эшелонов защиты. Это приводит к необходимости разработки второго варианта модели воздействия.

Вариант 2. Простая эшелонированная модель защиты информации (рис. 2.2).

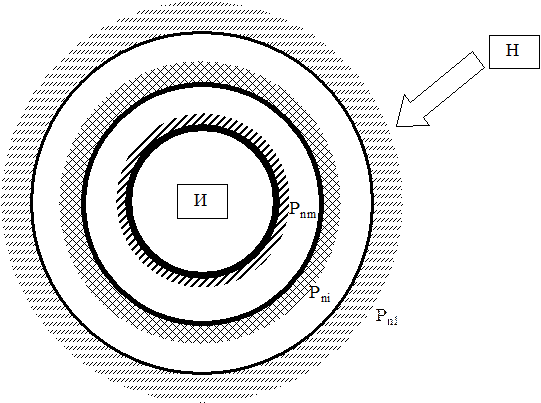
Рисунок 2.2 - Простая эшелонированная   модель воздействия нарушителя

Используемые ограничения и допущения:

1) нарушитель пытается завладеть информацией,  хранящейся за m эшелонами защиты, совершая ограниченное k число независимых попыток воздействия;

2) все эшелоны защиты однородны, круговые и действуют постоянно;

3) вскрытый эшелон защиты не восстанавливается.