Оценки максимального правдоподобия. Ковариационные матрицы вектора ошибок обеих оценок. Байесовская оценка

5.5 Оценки максимального правдоподобия.

Пусть теперь оцениваемый вектор х либо является неслучайным, либо случайным, но с неизвестной ПРВ f(x).

Согласно принципу МП за оценку  принимается такое значение, при котором вероятность реализовавшегося наблюдения наибольшая.

Если f(z/x) - условная ПРВ при фиксированном значении параметра х, то при фиксированном значении вектора z, реализовавшемся в процессе испытания, функция L(x)=f(z/x) называется функцией правдоподобна.

Оценка МП ищется из условия

                                                          (5.5.1)  или                                                     

в случае независимых результатов наблюдений, поскольку в этом случае

                                              (5.5.2)

Оценка МП ищется обычно из системы уравнений

, где         

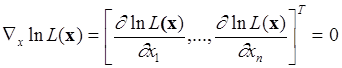                                                 (5.5.3)

Если компоненты z₁, ..., z_n вектора z независимы, то

.

Любое решение системы (5.5.3), зависящее от z и удовлетворяющее

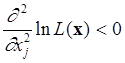
называется оценкой МП.

Поскольку

и f(z) от вектора х не зависит, то оценка МАВ являлась решением задачи

или       

 , откуда

                                                         (5.5.4)

Если о параметре х априорная информация отсутствует, то оценку МАВ получить невозможно без дополнительных предположений.

Предположение о равновероятности всех возможных значений х, т.е. f(x)=const приводит к

и МАВ оценка является корнем уравнения

,                   

  (5.5.5)

т.е. оценкой МП.

Получили выражение оценки максимального правдоподобия для рассмотрения в примере 5.1 линейной схемы наблюдения, трактуя оцениваемый вектор как неслучайный, и сравним оценку МП с полученной байесовской квадратичной оценкой.        

Пример 5.4

z=Hx+v,

v~

Вектор х считаем неслучайным.

Имеем

.

Поскольку шум v не зависит от х, то

, поэтому

 

таким образом, функция правдоподобия имеет вид

Оценка МП является корнем уравнения

.

, если и только

 

В итоге получим

                                   (5.5.6)

Полезно сравнить оценку МП (5.5.6) с оценкой МАВ (5.4.8).

,     

Если положить в (5.4.8)

, то получим :

    (5.5.7)

Ковариационные матрицы вектора ошибок обеих оценок равны

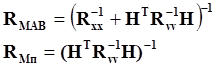
Поскольку ковариационные матрицы положительно определённые, то

, так как

.

Поэтому

                      (5.5.8)

то есть матрица ковариации ошибки среднеквадратичной оценки всегда меньше, чем оценки МП. Кроме того,

, т.е. обе оценки являются несмещенными.

1.   Рассмотрим частный случай единичной матрицы наблюдений, когда H=I, т.е. управление наблюдения имеет вид

z=x+v.

Тогда, используя общие выражения для оценок, в этом частном случае будем иметь: оценка максимального правдоподобия равна

                                                                     (5.5.9)

Байесовская оценка в данном случае равна

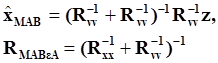                                                                    (5.5.10)

Таким образом, в данном случае МП оценка не оправдывает ожиданий и просто совпадает с вектором наблюдений.

2.   Пусть  т.е. оценивается скалярный параметр х в схеме

и

х~

v~

Байесовская оценка, согласно результату примера 5.1. имеет вид

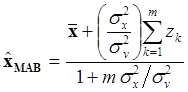                                                                        (5.5.11)

и

                                                       (5.5.12)

Оценка максимального правдоподобия равна

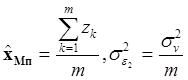                                                                        (5.5.13)

Анализ полученных выражений показывает, что с увеличением объема выработки оценка максимального правдоподобия приближается к байесовской оценке и при  точность оценок практически совпадает.

5.6 Оценивание параметров методом наименьших квадратов.

Пусть

u^T=[u₁, ..., u_q] - вектор независимых величин, которые могут быть фиксированными, либо управляемыми,

z^T=[z¹, ..., z_m] - вектор зависимых величин, доступных наблюдению, тогда механизм связи между величинами u и z может быть описан уравнением следующего вида

z = F(u, x) ,                                         (5.6.1) где х^Т=[х₁, ..., х_n] - вектор параметров, не доступных наблюдению, но в соответствии с (5.6.1) характеризующих протекание процесса.

Из-за неизбежных ошибок измерения величин u, отсутствия полной информации о протекающих процессах, ошибок в измерении моментов времени фиксации зависимости отличается от истинной. Кроме того, измерение величин z всегда сопровождается ошибками, поэтому уравнения модели имеют вид