Электротехника \ Теория решения изобретательских задач

Оценки максимального правдоподобия. Ковариационные матрицы вектора ошибок обеих оценок. Байесовская оценка, страница 2

z = F(u, x)+v , (5.6..2) где v - вектор ошибок наблюдения, учитывающий как несоответствие вида функции истинному, так и объективно существующие ошибки измерения.

Выражение (5.6.2) принято называть управлением наблюдения. Если функция является линейной относительно оцениваемого вектора х, то уравнение наблюдения в этом случае является линейным.

В основе МНК лежит определение такого значения неизвестного параметра , которое объясняло бы появление в результате эксперимента значения вектора z, и обеспечивало наименьшее значение суммы квадратов невязок, т.е. определяется из условия минимизации по х величины

I(x)=[z-F(u, x)]^T[z-F(u, x)]

Решение задачи

приводит к системе уравнений

, (5.6.4) которая называется нормальной.

Рассмотрим простейшие примеры получения уравнений наблюдения.

Пример 5.5

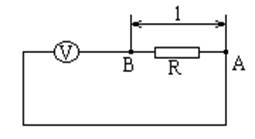
Рис.5.6.1

Пусть z(l) - падение напряжения между точками А и В (рис.5.6.1). В точках l₁, l₂, ..., l_m

измеряют величины z(l_k), пропорционально току цепи:

, где - ошибка измерений,

- удельное сопротивление проводника,

j=1(1)m

или

, где

Таким образом, после “m” измерений имеем:

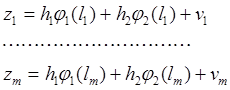
или

, (5.6.4)

где

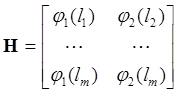- матрица наблюдений размером (mx2)

Модель вида

при отсутствии ошибок измерения является точной, поскольку получена из физических соображений. Вектор

ищется из условия

, где z - вектор реализовавшихся измерений,

Нх- вектор неискаженных ошибками измерений.

Пример 5.6

Пусть (x_k, z_k) пары наблюдений случайных переменных, где x_k - значения “независимой” случайной величины. Построение функции регрессии E(z/x)=f(x) требует многократного измерения величины y в каждой точке x_k, что может оказаться невозможным. Поэтому регрессионную модель строят в заданном классе функций в виде

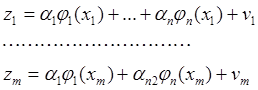(5.6.5)

или , где - вектор измеренных значений зависимой переменной z,

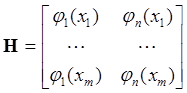- матрица наблюдений размером (mxn)

- вектор искомых параметров,

- вектор ошибок измерения.

Вектор невязок z-Hx содержит как ошибки модели, обусловленные произволом в задании класса функций, так и ошибки собственно измерений. Минимизация по х позволяет определить такое значение , которая дает наилучшую аппроксимацию в смысле наименьших квадратов зависимости f(x) в классе .

Пример 5.7

Оценка параметров сигнала. Пусть s(t) - выборочная функция некоторой совокупности, доступная измерению в моменты времени t_k, с ошибками , т.е.

(5.6.6)

Отсутствие априорной информации о статистических характеристиках процесса s(t) приводит к заведомо неточной модели наблюдения. Модель сигнала которая строится в виде линейной комбинации конечного набора линейно не зависимых функций ,т.е.