Оценки максимального правдоподобия. Ковариационные матрицы вектора ошибок обеих оценок. Байесовская оценка, страница 5

Вектор остатков равен

         (5.6.27)

Остаточная сумма квадратов

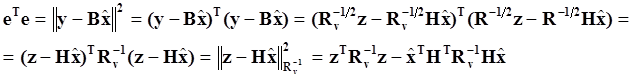
(5.6.28)

Из выражения (5.6.26) определяем вектор ошибки оценивания

                                                     (5.6.29)

Остаточная дисперсия ошибки оценки равна

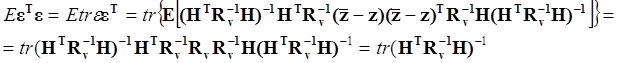
(5.6.30)

Ковариационная матрица оценки (ошибки оценки) равна

Таким образом, НЛНО в общем случае определяется выражением (5.6.24) или (5.6.26).

Рассмотрим некоторые важные частные случаи ошибок измерения в общей схеме обобщённых оценок.

1.   - равноточные некоррелированные наблюдения. Положим

, тогда уравнение наблюдения можно записать

, где 

НЛНО имеет вид

или

                                                                                 (5.6.31)

Вектор остатков равен:

Остаточная сумма квадратов:

Вектор ошибки:

                                                              (5.6.32)

Ковариация ошибки:

                                                                        (5.6.33)

Остаточная дисперсия оценки:

                                           (5.6.34)

2.                                                 , 

- случай равноточных коррелированных наблюдений.

Положим

N=KK^T

И

, тогда можно записать

, где 

Оценка (НЛНО) имеет вид

                         или            (5.6.35)

Ковариация ошибки:

                                                                    (5.6.36)

Остаточная дисперсия оценки:

                                                             (5.6.37)

3.   - неравноточные некоррелированные наблюдения.

Пусть 

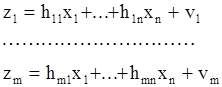
или                                          

, где ,

,

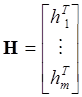Оценка записывается в общем виде (5.6.24)

или более подробно

, откуда получим окончательное выражение для оценки

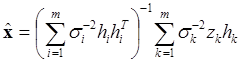                                                               (5.6.38)

Критерий оценивания при этом имеет вид

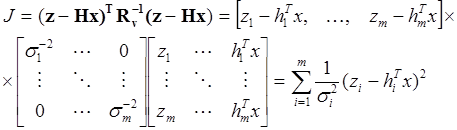                      (5.6.39)

Таким образом, оценка (5.6.38) минимизирует взвешенную сумму квадратов отклонений наблюдений  от их математических ожиданий .

Ковариация ошибки:

Остаточная дисперсия оценки:

Полезно и поучительно провести сравнительный анализ оценок МНК с байесовскими оценками и оценкой максимального правдоподобия для линейной схемы наблюдений и нормального распределения вектора ошибок с ковариационной матрицей R_v.

Оптимальная байесовская оценка оказалась инвариантной к виду функции потерь линейной функцией результатов наблюдений. При

и независимых с оцениваемым вектором ошибках наблюдения, согласно (5.4.8) можно записать выражение для этой оценки

                                                           (5.6.40)

Ковариационная матрица вектора ошибок равна

Сравнивая выражения (5.5.6) и (5.6.25) приходим к выводу, что для линейной схемы наблюдения и нормально-распределённого вектора ошибки МП-оценка и МНК-оценка совпадают между собой и равны

, и

                                                                            (5.6.41)

Из записанных выражений следует, что если в (5.6.40) и (5.6.41) принять , что означает неограниченное возрастание дисперсий всех компонент х_iвектора х, и как следствие отсутствие априорной информации о величинах х_i , то автоматически получаем оптимальные МП и МНК оценки, в которых оцениваемый вектор в постановочной части обоих методов оценивания трактовался как неслучайный. Это оправдывает оправдывает возможность интерпретации неслучайного вектора как случайного с некоррелированными компонентами и бесконечно большими дисперсиями.