Оценки максимального правдоподобия. Ковариационные матрицы вектора ошибок обеих оценок. Байесовская оценка, страница 3

                                                z=y+v                                             (5.6.7)

где y=Hx - вектор “правильных” измерений, который имел бы место при точной модели наблюдения, и отсутствии ошибок наблюдения; тогда полагая вектор х неслучайной величиной, получим :

                                                                        (5.6.8)

где  по предположению.

Ошибки наблюдений характеризуются ковариационной матрицей

Рассмотрим некоторые случаи:

1.    - равноточные некоррелированные наблюдения. Случай соответствует ситуации независимых между собой измерений одинаковыми приборами. Величина  известна, или подлежит определению.

2.   , где N - известная нормированная ковариационная матрица, соответствует случаю равноточных, но коррелированных наблюдений.

Полагая  N=kk^T,  получим схему

, где , причем .

Таким образом, данная схема равноточных коррелированных наблюдений заменой координат приводится к случаю 1.

3. 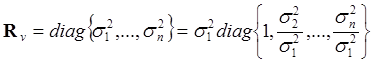  -случай неравноточных некоррелированных наблюдений, приводится к случаю 2.                          

4.   Общий случай соответствует произвольной симметричной неотрицательно определённой ковариационной матрице

                                                                                         (5.6.9)

Для оценки точности результатов необходимо знание R_z, либо задание R_v в виде , с последующей оценкой величины .

5.6.2 Простейшие оценки МНК

Пусть              

                                        z=Hx+v ,                                             (5.6.10)

- линейная схема наблюдений где     H - (m x n) – матрица наблюдений,

x - (n x 1) – вектор неизвестных параметров

z - (m x 1) – вектор результатов наблюдений

v - (m x 1) – вектор ошибок наблюдений, причём

                                                ,                               (5.6.11)

т.е. рассматривается случай равноточных некоррелированных наблюдений. 

Вектор неискаженных помехами измерений есть

.

Если бы этот вектор был известен, то оценка вектора х имела бы вид H⁺z^* в смысле

, где H⁺ - псевдообратная в смысле Мура-Пенроуза матрица.

Пытаемся искать оценку , которая объясняла бы появление в результате опыта реализовавшееся значение вектора z, из условия

                        (5.6.12)

Условие (5.6.12) имеет ясный геометрический смысл: пусть

R_H={Y: Hx=y}

-  множество значений преобразования с матрицей Н. Тогда критерий (5.6.12) минимизирует квадрат расстояния от вектора наблюдений z до подпространства R(H). Квадрат длинны этого вектора

достигнет минимума при том значении , при котором перпендикулярно R(H). Другими словами, вектор

представляет собой ортогональную проекцию вектора наблюдений, на множество R(H)  (рис.5.8.1).

Рис.5.6.2

Рис.5.8.1

Имеем

                           

откуда

                                                                                                                         (5.6.13)

Равенство (5.6.13) представляет собой условие ортогональности.

Уравнение (5.6.13) называется нормальным уравнением и всегда имеет решение, поскольку

,

где R(Н) – множество значений матрицы Н, состоящее из векторов вида Нх при .

Любое решение уравнения (5.6.13) имеет вид:

, где w- произвольный (n x 1) вектор.

Вектор, доставляющий решение задачи и имеющий минимальную норму равен

                                                       (5.6.14)

Этот единственный вектор нормальным псевдорешением линейной системы