1. Y(t) измеряется динамически.
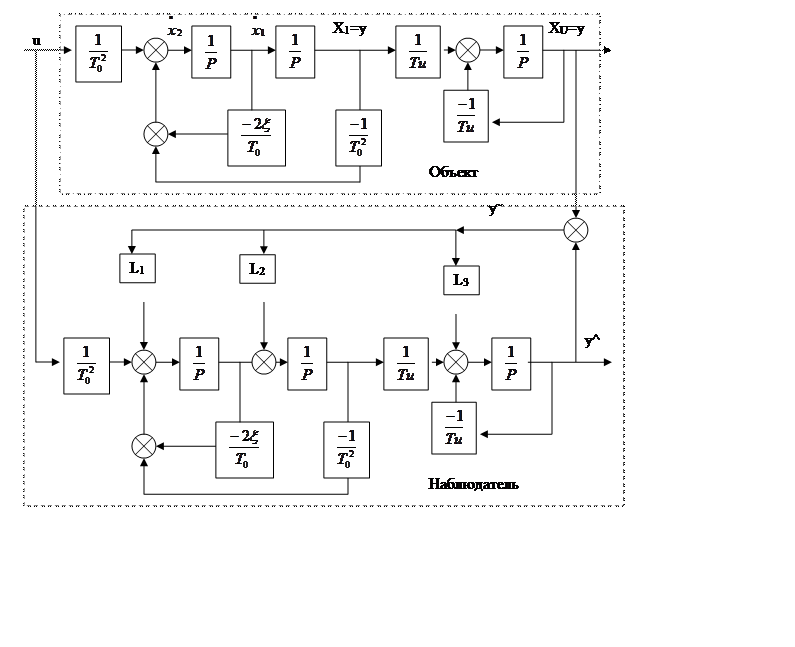
Из схемы запишем:
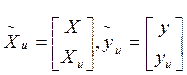
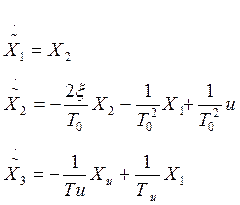
Получаем:
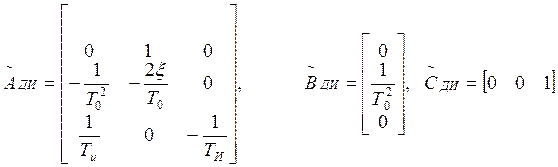
Для медианных значений получаем:
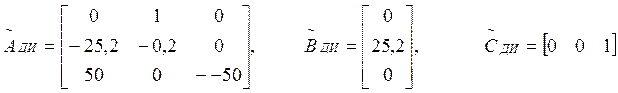
Динамические наблюдающие устройства
полной размерности в базисе исходного объекта вектора ![]() состояния
непрерывного объекта управления (4.1), реализующее алгоритм наблюдения,
записываемый в векторно-матричной форме
состояния
непрерывного объекта управления (4.1), реализующее алгоритм наблюдения,
записываемый в векторно-матричной форме
![]() ,
,
Невязка наблюдения:
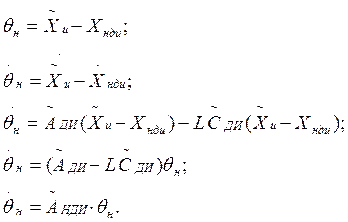
Назначаем желаемую структуру собственных значений матрицы
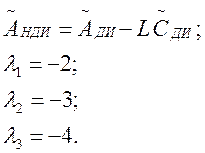
Н - произвольная матрица ![]() – наблюдаемая пара матриц,
– наблюдаемая пара матриц, ![]()
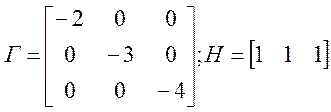
Матрицу ![]() ,
вычисляем, решая матричное уравнение Сильвестра
,
вычисляем, решая матричное уравнение Сильвестра
![]()
![]()
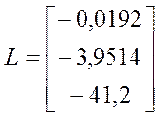
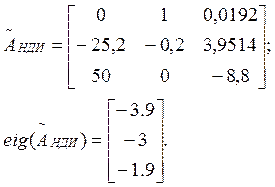
Собственные значения вычисленной
матрицы ![]() совпадают с желаемыми, следовательно
матрица L найдена верно.
совпадают с желаемыми, следовательно
матрица L найдена верно.
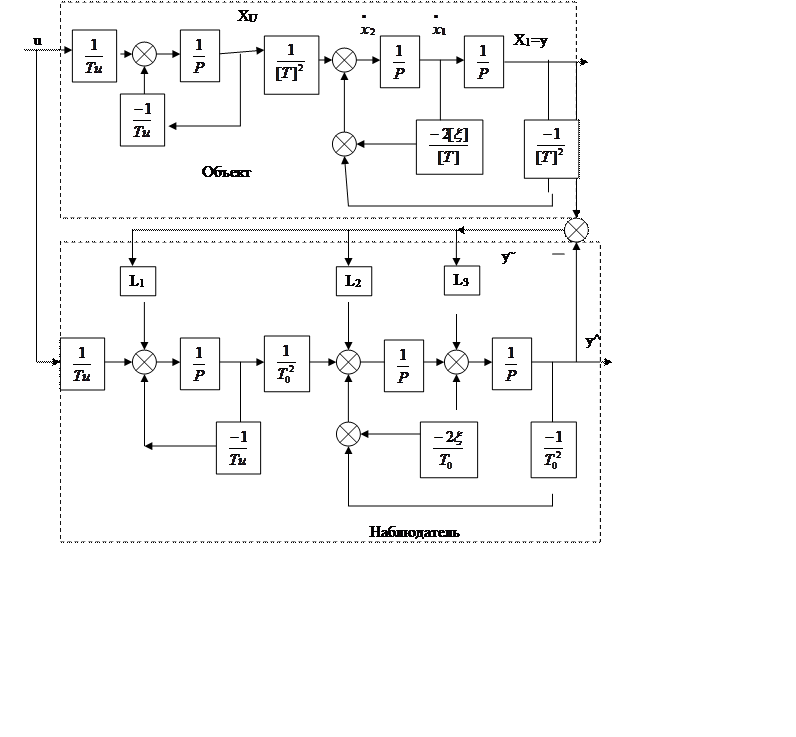
Схема моделирования:
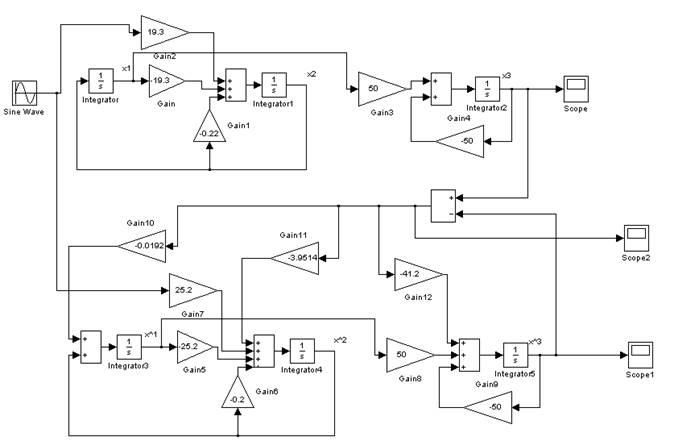
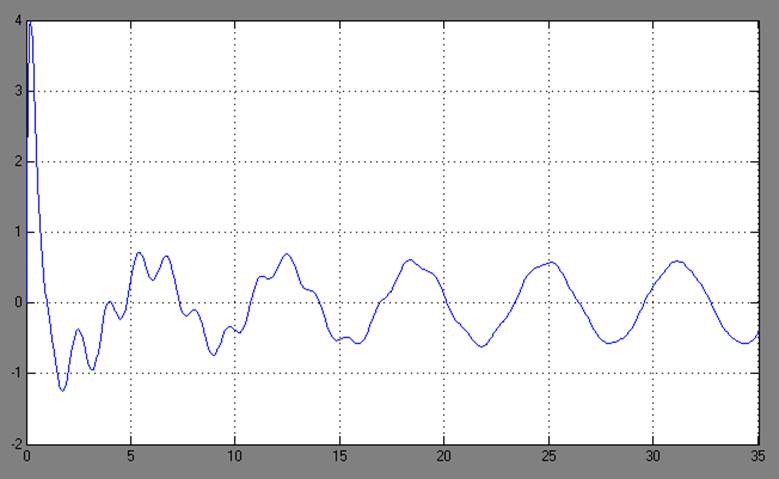
Результаты:
1) для медианных значений и ненулевых начальных условий
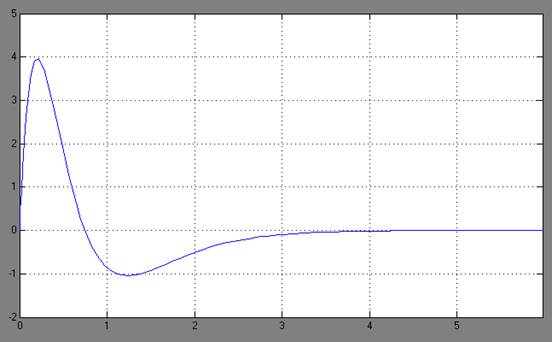
Ошибка оценивания
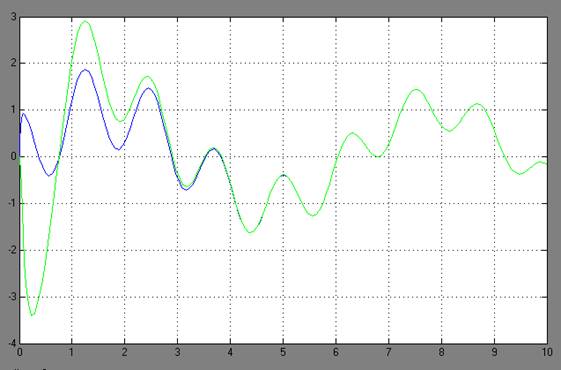
На графике зеленый - выход наблюдателя (оценка), синий – выход объекта с динамическим измерителем.
2) для «крайней левой» реализации параметров
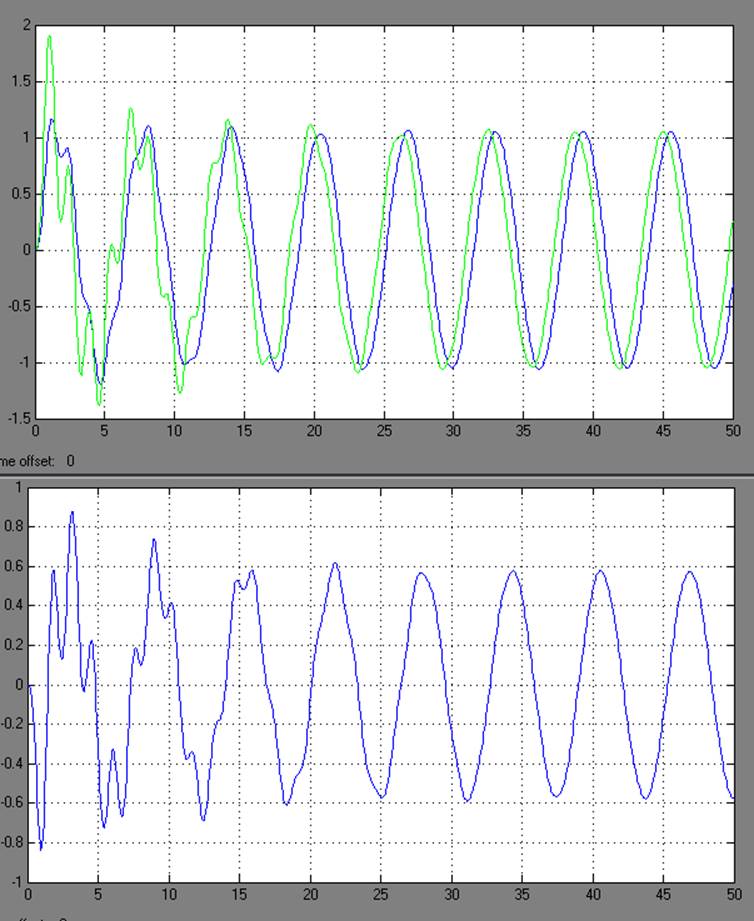
На 1 графике зеленый - выход наблюдателя, синий – выход объекта с динамическим измерителем. На втором – ошибка.
3) для «крайней правой» реализации параметров
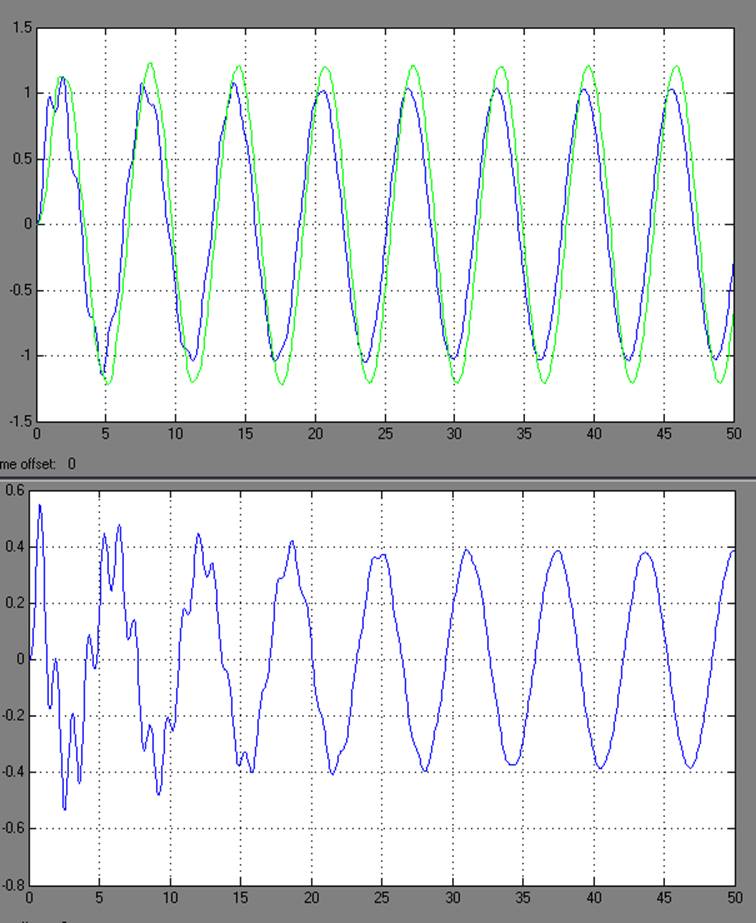
На 1 графике зеленый - выход наблюдателя, синий – выход объекта с динамическим измерителем. На втором – ошибка.
Как видно из графиков, инерционность измерительного
устройства не влияет на наблюдение параметров. Также видно, что ошибка
оценивания не сходится к нулю, вследствие вариации значений параметров ![]() и
и ![]() ,
которые мы не учитываем в наблюдательном устройстве.
,
которые мы не учитываем в наблюдательном устройстве.
Введем в рассмотрение невязку невязки наблюдения ![]() , порожденную вариацией.
, порожденную вариацией.
|
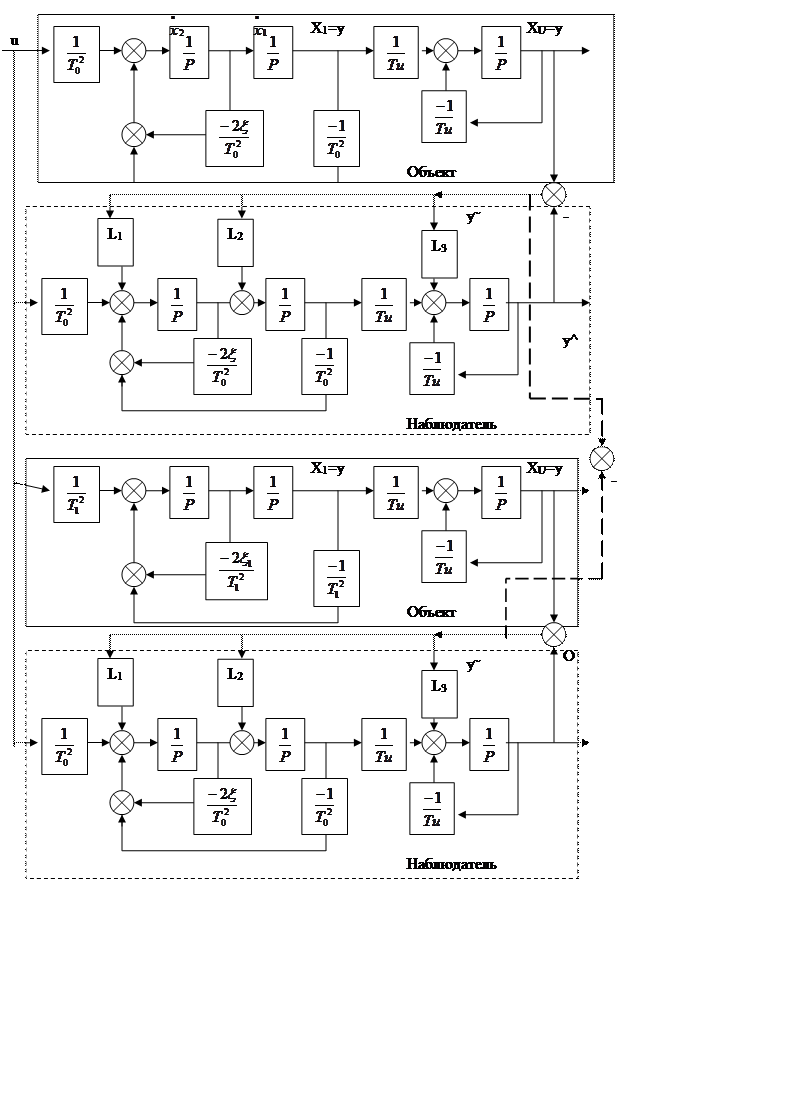
Получаем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.