,канонические формы матриц. Матрицы приведения подобия. Блочно-диагональная каноническая форма матрицы

Диагональная каноническая форма матрицы может быть построена, когда алгебраический спектр собственных значений имеет реализацию

.                   (4.2)

Алгебраический спектр вида (4.2) порождает множество подобных матриц линейного оператора A , именуемых матрицами простой структуры.

В случае реализации алгебраического спектра   в форме (4.2), когда все собственные значения вещественные и простые (различные, не кратные), может быть построена диагональная матрица  с элементами  на главной диагонали и нулями на остальных позициях этой матрицы так, что она принимает вид

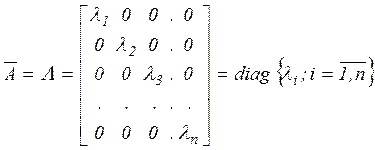.                        (4.3)

2.Блочно-диагональная каноническая форма матрицы может быть построена, когда алгебраический спектр собственных значений имеет реализацию

 (4.4)

В случае реализации алгебраического спектра   в форме (4.4), когда все собственные значения комплексно-сопряженные и простые (не кратные), может быть построена блочно-диагональная матрица  с вещественнозначными матричными блоками 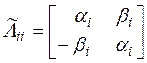 на главной диагонали и нулями на остальных позициях этой матрицы так, что она принимает вид

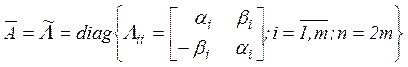.                  (4.5)

3. Комбинированная блочно-диагональная каноническая форма матрицы может быть построена, когда алгебраический спектр собственных значений содержит только простые собственные значения, часть которых числом  являются вещественными, а другая часть числом - комплексно-сопряженными, при этом выполняется соотношение

Комбинированная блочно-диагональная матрица имеет на своей главной диагонали диагональную матрицу вида (4.3) размерности  и блочно-диагональную матрицу вида (4.5) размерности так, что она примет вид

                     (4.6)

Матричные блоки на диагонали комбинированной блочно-диагональной матрицы можно менять местами, так что наряду с формой (4.6) матрица  может иметь представление

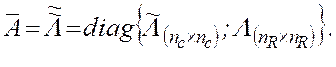                        (4.7)

Так например, если алгебраический спектр собственных значений матриц ЛО A  имеет реализацию

,     (4.8)

то комбинированное блочно-диагональное представление канонической матрицы  принимает вид

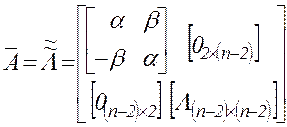                                           (4.9)

где- соответственно нулевые матрицы размерности и диагональная матрица размерности .

4. Жорданова каноническая форма матрицы может быть построена, когда алгебраический спектр собственных значений имеет реализацию

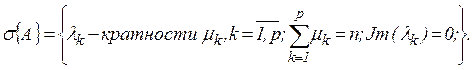    (4.10)

Тогда жорданова каноническая форма матрицы  максимально близкая к диагональной форме для случая вещественных кратных собственных значений матриц ЛО A  в соответствии со структурой алгебраического спектра (4.10) примет вид

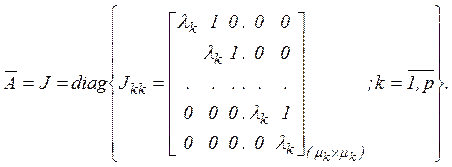        (4.11)

Жорданова каноническая форма (4.11) представляет собой блочно-диагональную матрицу, составленную из жордановых блоков размерности , имеющих на своей главной диагонали собственное значение  кратности , единицы на первой наддиагональю и нули на остальных позициях блока. Жорданова каноническая форма (4.11) является верхней жордановой формой, наряду с которой может быть построена нижняя жорданова каноническая форма, которая характеризуется тем, единицы жордановых блоках размещаются на первой поддиагонали. Следует заметить, что жорданова каноническая форма может быть построена и для случая матриц ЛО, алгебраический спектр собственных значений которых содержит кратные комплексно-сопряженные элементы, причем возможны как комплексно-значная так и вещественно-значная формы.

5.Рассмотрим теперь канонические представления  исходной матрицы , которые конструируются на алгебраическом спектре  коэффициентов характеристического полинома

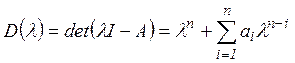                              (4.12)

матриц  линейного оператора A .Этих представлений два, они совпадают с точностью до транспонирования. Канонические имеют вид

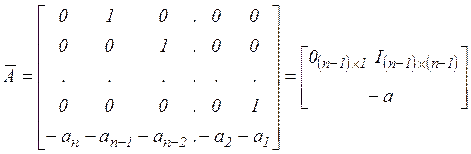    (4.13)

и

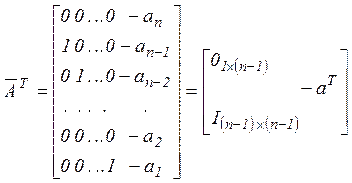.                           (4.14)

В канонических формах (4.13) и (4.14) - -мерный вектор-строка коэффициентов, записанных в обратном по отношению их размещения в характеристическом полиноме порядке так, что он принимает вид

,        (4.15)

соответственно -мерные матрица-столбец и матрица-строка, а также единичная матрица.

Обе канонические формы (4.13) и (4.14) именуются нормальной, сопровождающей (свой характеристический полином) и фробениусовой канонической формой. С тем, чтобы их различать в тексте форму (4.13) целесообразно назвать строчной нормальной, сопровождающей или фробениусовой, а (4.14)- столбцовой. Целесообразно ввести для канонической формы (4.13) обозначение

Строчная сопровождающая каноническая форма матрицы ЛО A имеет в последней строке коэффициенты характеристического полинома, записанные с обратными знаками и в обратном порядке, первую наддиагональ, заполненную единицами, остальные позиции матрицы, заполненные нулями.

Столбцовая сопровождающая каноническая форма матрицы ЛО A имеет в последнем столбце коэффициенты характеристического полинома, записанные с обратными знаками и в обратном порядке, первую поддиагональ, заполненную единицами, остальные позиции матрицы, заполненные нулями.

Теперь дадим ответ на второй вопрос, поставленный в начале раздела, то есть построим матрицы приведения подобия произвольной матрицы ЛО A  к каноническим формам.

Приведение матрицы  простой структуры ЛО A к диагональной форме (4.3) строится на положениях следующих утверждений.

Утверждение 4.1(У4.1).Матрица , приводящая произвольную  квадратную матрицу  простой структуры ЛО A  к диагональной форме в силу соотношения (4.1), принимающего для представление

,                                                                  (4.16)

имеет своими столбцами собственные векторы матрицы

Доказательство. Запишем базовое уравнение матричного подобия для рассматриваемого случая

                                                                       (4.17) в столбцовой форме

              (4.18)

где -  столбцы соответственно матриц Перейдем теперь от матричного уравнения (4.18) к векторно-матричным уравнениям вида

,                                                   (4.19)

где столбец диагональной матрицы имеет вид

                                                    (4.20)

Нетрудно видеть, что с учетом (4.20) векторно-матричное уравнение (4.19) принимает вид

                                                   (4.21)

Векторно-матричное соотношение (4.21) является определением собственного вектора матрицы , откуда следует