Санкт-Петербургский Государственный Университет
Информационных Технологий Механики и Оптики
Кафедра Систем Управления и Информатики
Лабораторная работа №5
" Абсолютно устойчивые системы" и
« Гиперустойчивые системы»
|
Выполнил: |
Студент гр. 4148 |
|
Преподаватель: |
|
Санкт - Петербург
2008
1. Абсолютно устойчивые системы
Исследовать нелинейную систему, состоящую из линейного блока:
![]() ,
,
с входом u и выходом y=x1 и нелинейного статического блока:
![]() ,
,
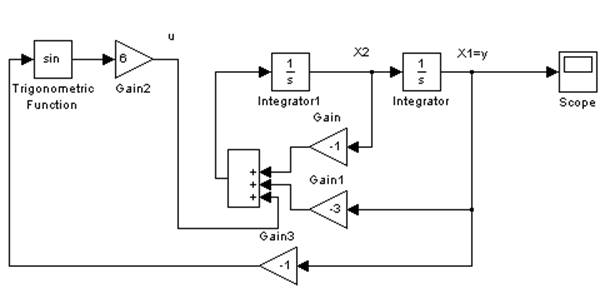
Рисунок 1- Схема моделирования.
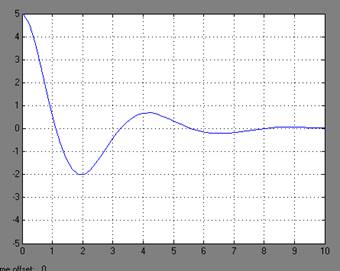
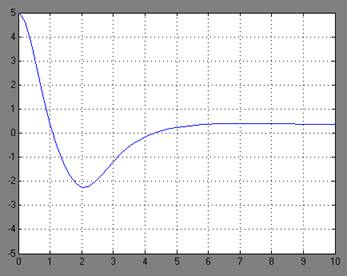
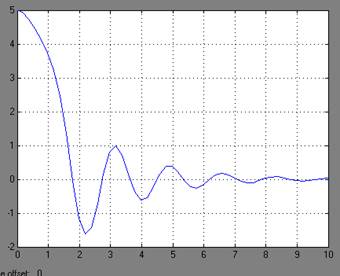
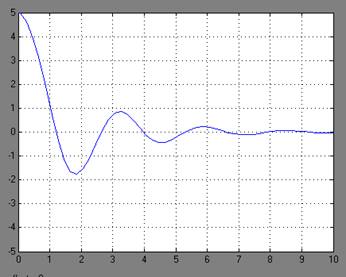
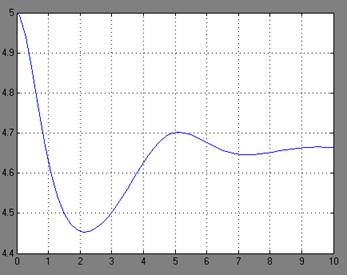
Рисунок 2 – Графики переходных процессов y(t) при различных значений а=-3;-1; 4; 11; 14 и для начальных условий х1(0)=5, х2(0)=0.
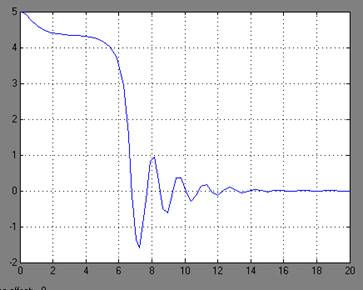
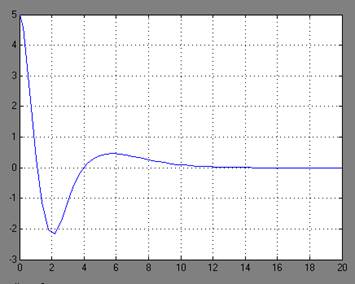
Рисунок.3 - Графики переходных процессов y(t)
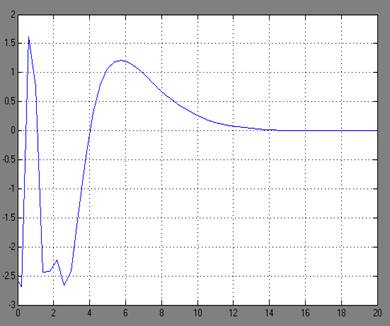 для граничных устойчивых состояний при а= -2.7 и а=13.9.
для граничных устойчивых состояний при а= -2.7 и а=13.9.
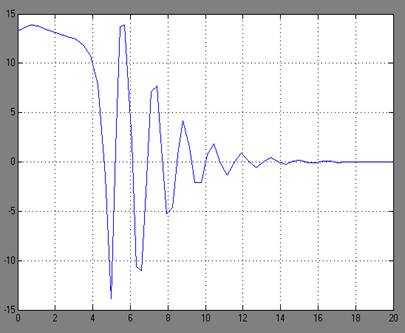
Рисунок 4 - Графики функции f(v) соответствующие предельно допустимым значениям а:
а=-2,7 а= 13,9
2. Гиперустойчивые системы
Исследовать нелинейную систему, состоящую из линейного блока:
![]() ,
,
с входом u и выходом
![]()
и динамического блока:
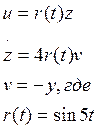
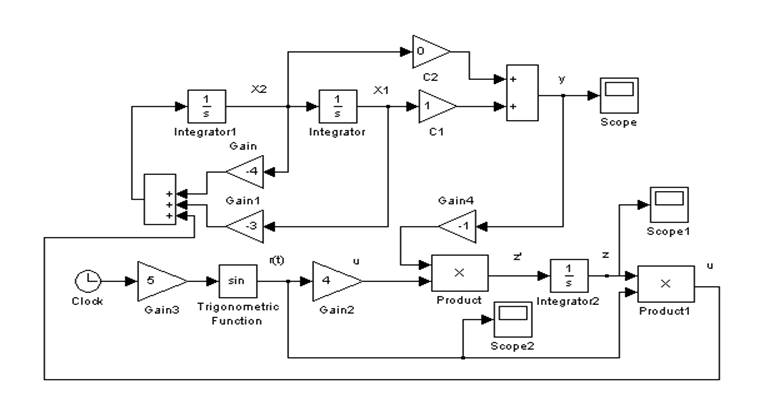
Рисунок 5- Схема моделирования.
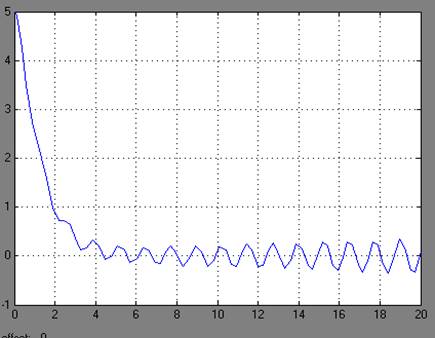 а) с1=1, с2=0
а) с1=1, с2=0
Рисунок.6 - График переходного процесса y(t)
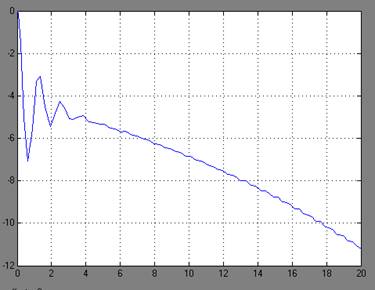
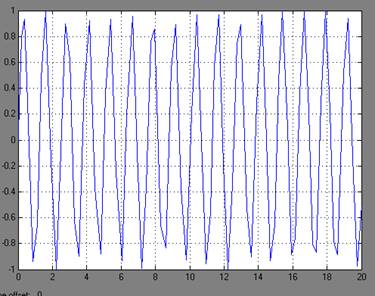
Рисунок 7 - Графики переходных процессов z(t) и r(t)
Вывод: система неустойчива.
б) с1=1.5, с2=1
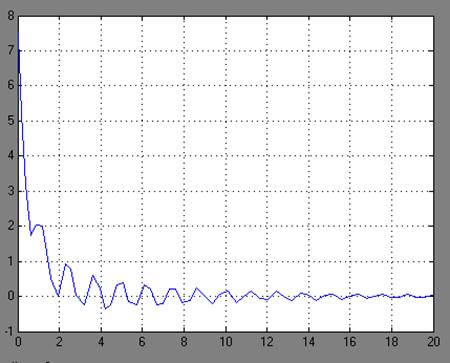
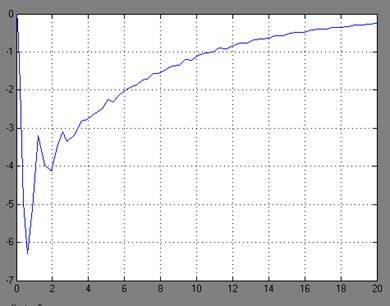 Рисунок.8 - График переходного процесса y(t)
Рисунок.8 - График переходного процесса y(t)
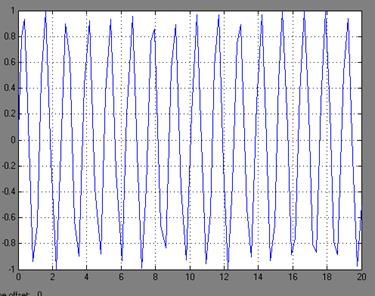
Рисунок 9 - Графики переходных процессов z(t) и r(t)
Вывод: система устойчива
Векторно-матричная форма системы имеет вид:
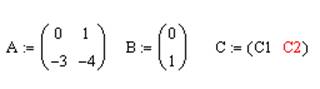
Передаточная функция W(p):
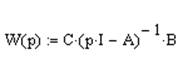
а) ![]()
Полюса системы: p=-3 и p=-1
Нулей системы нет.
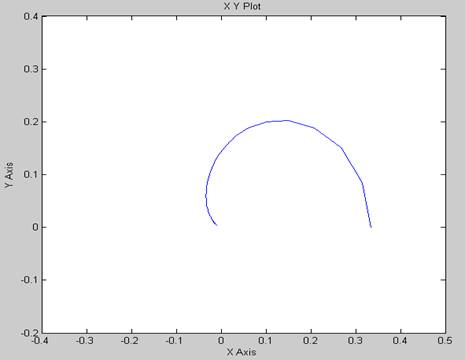
Рисунок 10 – АФЧХ
б)
![]()
Полюса системы: p=-3 и p=-1
Нулей системы: p=-1.5
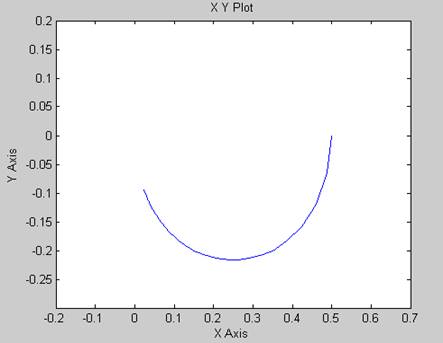
Рисунок 11 – АФЧХ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.