Точная линеаризация и стабилизация выхода. Попятный синтез и стабилизация каскадных систем. Точная линеаризация и стабилизация выхода

 Санкт-Петербургский Государственный Университет

Информационных Технологий Механики и Оптики

Кафедра Систем  Управления  и Информатики

Нелинейные и оптимальные системы

Лабораторная работа № 7

«Точная линеаризация и стабилизация выхода.  Попятный синтез и стабилизация каскадных систем».

Санкт-Петербург

2008 г.

Цель работы: для заданных систем вычислить алгоритм точной линеаризации и стабилизировать систему с заданными параметрами качества переходного процесса. Стабилизировать каскадную систему методом попятного синтеза (backstepping).

Исследование:

1.  Точная линеаризация и стабилизация выхода.

В нормальной форме модель внешней динамики нелинейной системы представляется в виде:

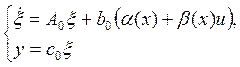                                                                                  (1)

Заданные системы имеют единичную относительную степень, следовательно:

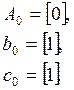                                                                                                                 (2)

В общем виде алгоритм точной линеаризации системы, приведенной к нормальной форме записывается так: , где                                                                                                 (3)

В этом случае система представима в эквивалентной линейной форме:

                                                                                                       (4)

Или с учетом относительной степени для заданных систем: , где - новое управляющее воздействие.

Полученная линеаризованная модель системы стабилизируется с помощью алгоритма управления

                                                                                              (5)

Определим параметры управляющего воздействия, обеспечивающие заданные показатели качества. Для полученной линеаризованной модели можно записать.

 Для  получаем

Полное описание регулятора для исходной системы имеет вид:

, где                                                             (6)

Для заданных систем

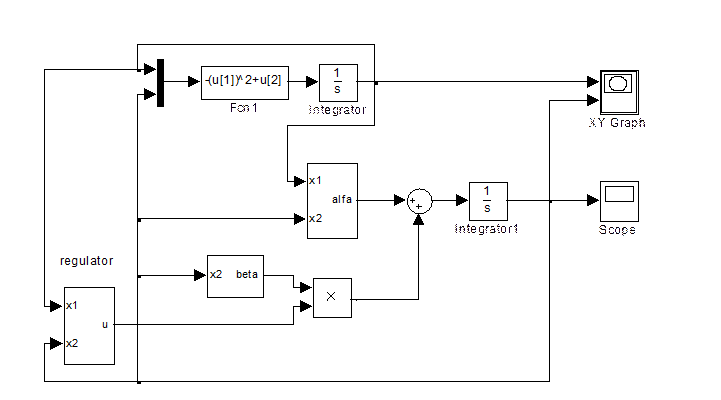
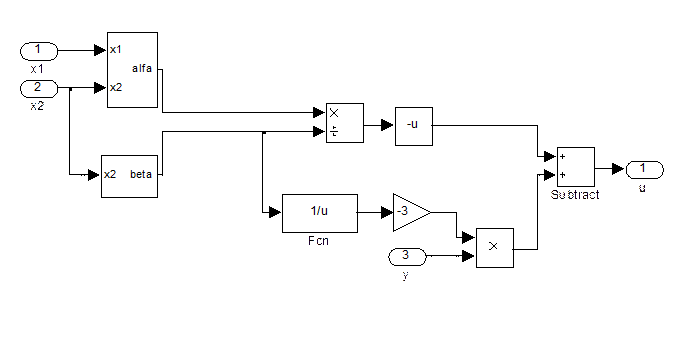
Рис.1- Типовая схема моделирования.

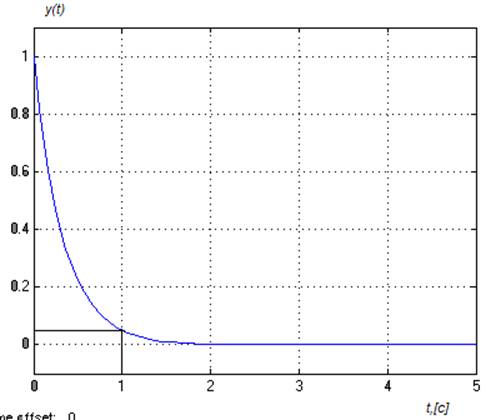
Рис.2- переходные процессы системы.

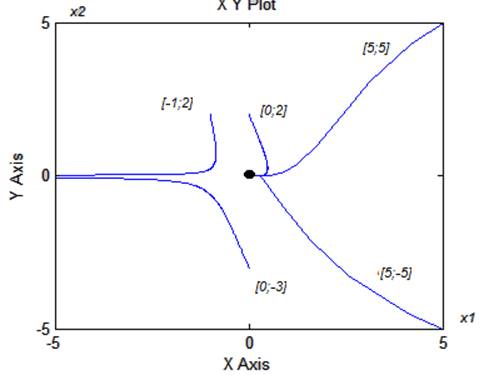
Рис.3-Фазовый портрет ОУ1.

В случае, если  нуль-динамика заданной системы обладает  свойством устойчивости и полноты в некоторой окрестности, то замкнутая система, приводимая к нормальной форме,  локально асимптотически устойчива по выходу.

2.  Попятный синтез и стабилизация каскадных систем.

В заданном объекте управления:

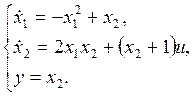                                                                                                 (8)

Возьмем

Тогда система представима как каскадная в форме:

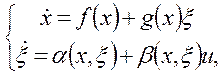                                                                                          (9)

Или                                                                                                                            (10)

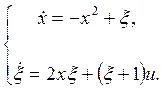                                                                                                     (11)

·  В предположении, что - желаемое управление, найдем виртуальное управление, обеспечивающее стабилизацию подсистемы (10):

                                                                               (12)

Для заданной системы стабилизирующее воздействие имеет вид:

                                                                            (13)

В этом случае  модель (10) примет вид  И при  замкнутая система асимптотически устойчива. Для обеспечения времени переходного процесса 1с выберем .

Введем в рассмотрение ошибку:

                                                                                  (14)

Тогда подсистема (10) записывается в виде:

                                                                            (15)

Продифференцируем (14):

                                                                (16)

где

Для заданной системы (10)-(11)

                                                                                (17)

                                  (18)

При выборе алгоритма стабилизации ошибки в виде:

                                                      (19)

Получим линейную модель ошибки

Для обеспечения требуемого времени переходного процесса стабилизации ошибки  выберем

В конечном виде для заданного ОУ стабилизирующее управление записывается в виде:                                                                     (20)

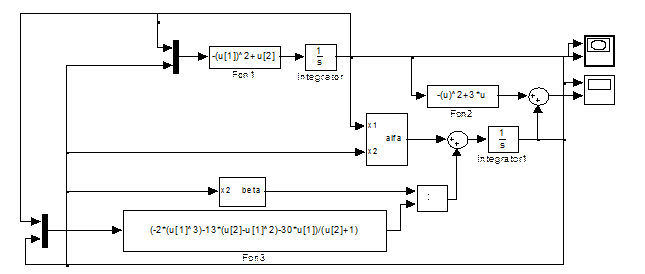
Рис.4- Схема моделирования каскадной системы.

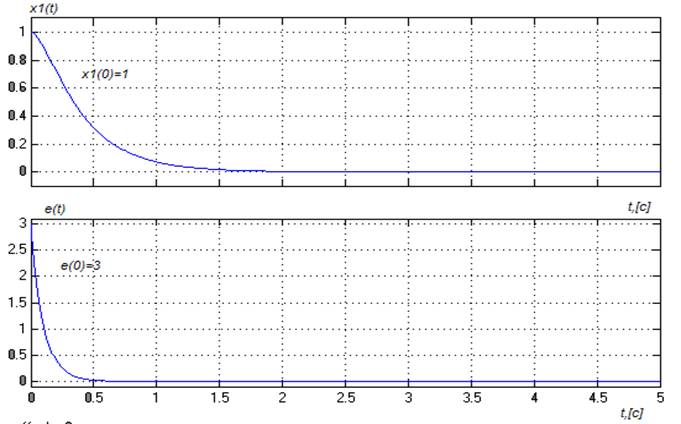
Рис.5- Переходные процессы стабилизированной замкнутой каскадной системы.

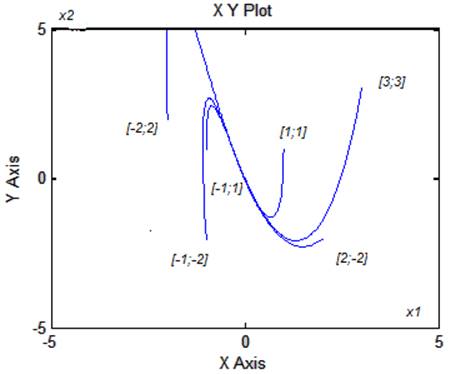
Рис.6-Фазовый портрет замкнутой системы.

Вывод: в ходе работы были получены стабилизирующие регуляторы для заданных объектов управления. Была изучена методика точной линеаризации нелинейных систем и метод попятного синтеза для каскадных систем. Результаты проведенного моделирования показали, что полученные регуляторы обеспечивают выполнение задачи управления с требуемыми параметрами переходных процессов.