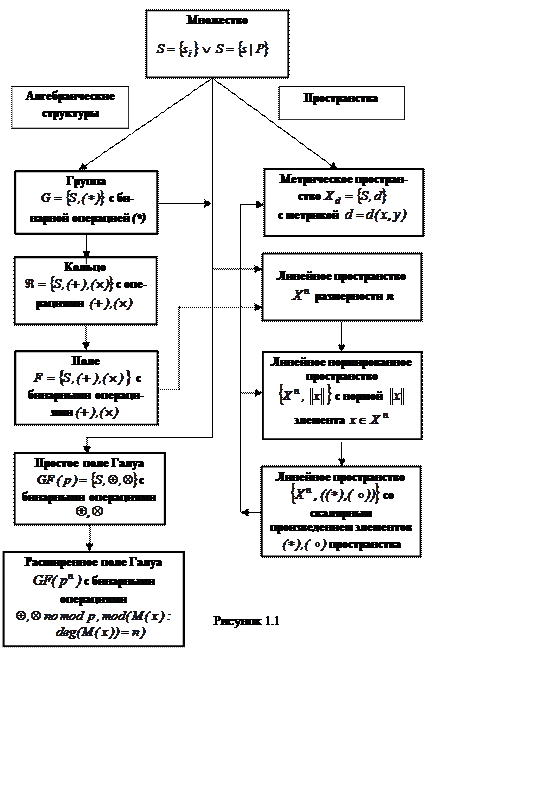
Алгебраические структуры. Мощность множества. Замкнутости относительно бинарной операции умножения

Алгебраической структурой называется множество с заданными в нем алгебраической бинарной операцией (или несколькими операциями) и свойствами элементов относительно этой бинарной операции.

В курсе МОТС изучаются следующие алгебраические структуры: группа (подгруппа), кольцо, идеал, поле, простое и расширенное поля Галуа.

Определение 1.4. Множество  называются группой, если для любой пары элементов множества  определена бинарная алгебраическая операция  и выполняются условия:

1.  Замкнутости: для , элемент ;

2.  Ассоциативности: для  

3.  Существования нейтрального элемента (единицы группы): G содержит единственный элемент

4.  Существования обратного элемента: для  (единственный для ), называемый элементом, обратным , такой, что .

Примечание 1.1:Группа  называется коммутативной или абелевой группой, если выполняется условие коммутативности: для .

Определение 1.5. Подмножество  группы  называется подгруппой, если оно удовлетворяет всем свойствам группы относительно бинарной алгебраической операции *.

Определение 1.6. Пусть  коммутативная группа,  подгруппа группы . Рассмотрим множество:

где .

Определенные таким образом множества называются смежными классами группы по подгруппе  и задают разложение группы  по подгруппе  с образующими элементами β_i, так что 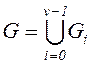, где число  называется индексом подгруппы  в группе .

Определение 1.7. Пусть имеются две группы  и  с бинарными операциями “” и “” соответственно одной и той  же мощности и  отображение  в  такое, что для всех  имеет место равенство: .

Отображение , обладающее таким свойством, называется изоморфным. Если между двумя группами и можно установить изоморфизм , то группы  и  называются изоморфными.

3 Определение 1.8 Множество  называется кольцом, если на нем определены бинарные алгебраические операции сложения и умножения и выполняются следующие условия:

1.  Множество является коммутативной группой относительно бинарной операции сложения;

2.  Замкнутости относительно бинарной операции умножения: для  элемент ;

3.  Ассоциативности относительно бинарной операции умножения: для ;

4.  Дистрибутивности относительно бинарных операций сложения и умножения: для

.

Примечание 1.2: Кольцо  называется коммутативным, если выполняется условие: .

Определение 1.9. Подгруппа J аддитивной группы  называется идеалом, если для  и  элемент .

Примечание 1.3: Идеал, состоящий из всех элементов, кратных некоторому элементу  кольца , называется главным  идеалом. Кольцо, в котором каждый идеал главный, называется кольцом главных идеалов. Элемент  называется образующим (или порождающим) элементом идеала.

Поскольку для кольца  справедливы все свойства группы, а для идеала  все свойства подгруппы относительно бинарной операции сложения, то кольцо  можно разложить подобно группе на смежные классы по идеалу .

Определение 1.10. Коммутативное кольцо  называется полем, если выполняются следующие условия:

1.  Кольцо  содержит нейтральный элемент 1 относительно бинарной операции умножения такой, что для   ;

2.  Для ,  существует обратный элемент .

3.  Если то  или

4 Определение 1.11. Если  – простое число, то кольцо чисел по  называется простым полем Галуа и обозначается .  состоит из элементов , таким образом .

Примечание 1.4. Определим на множестве  две бинарные операции:

сложения по , обозначив его , и умножения по, обозначив его :

1.  где- целое;

2.  , где- целое.

При этом  и  называются вычетами.

Определим понятия сравнимости по. Два целых числа  и  сравнимы по:

 где - целое.

1.12. Полином называется полиномом над полем или модулярным, если его коэффициенты  принадлежат простому полю . Степенью полинома  называется наибольшее число.

Примечание 1.5. Сравнение модулярных полиномов  и  по модулю модулярного полинома , производится аналогично сравнению целых чисел по  , где.

Аналогично можно ввести операции суммирования (вычитания), умножения по модулю модулярного полинома, при этом приведение подобных членов производится по modp. Так

, где , при этом  называется вычетом по .

Определение 1.13. Полная система вычетов по двойному модулю  образует конечное поле