Элементы линейной алгебры и аналитической геометрии. Метод Гаусса. Обратная матрица, после вычисления всех алгебраических дополнений

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Сибирский государственный индустриальный университет

Кафедра высшей математики

РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ

РАБОТ ПО КУРСУ «ВЫСШАЯ МАТЕМАТИКА»

1 семестр для студентов-заочников

___________________________________________________________

Издание СибГИУ                                                 Новокузнецк 1999

УДК 519.075

Даны примеры и рекомендации по выполнению контрольных работ 1-3 по высшей математике для студентов-заочников 1 курса по программе первого семестра.

Рецензент – кафедра физики Сибирского государственного инду-стриального университета ( зав. кафедрой профессор )

Печатается по решению редакционно-издательского совета  университета

ВВЕДЕНИЕ

Данные методические указания предназначены в помощь студентам-заочникам 1-го курса при выполнении ими контрольных работ по математике за 1 семестр (контрольные работы №1, №2, №3). Номера задач из сборника заданий распределены следующим образом:

Вари-ант	Номера заданий для контрольных работ
	№1	№2	№3
1 2 3 4 5 6 7 8 9 10	1    11    41    51 2    12    42    52 3    13    43    53 4    14    44    54 5    15    45    55 6    16    46    56 7    17    47    57 8    18    48    58 9    19    49    59 10   20   50    60	111  131 112  132 113  133 114  134 115  135 116  136 117  137 118  138 119  139 120  140	141  151 142  152 143  153 144  154 145  155 146  156 147  157 148  158 149  159 150  160

В конце данных указаний даны теоретические вопросы экзаменационных билетов за 1 семестр.

Контрольная работа 1

Тема: Элементы линейной алгебры и аналитической геометрии.

Задание 1. Даны векторы   в некотором базисе. Показать, что векторы  образуют базис и найти координаты вектора  в этом базисе.

Указания к решению. Векторы  будут образовывать базис, если определитель, составленный из координат этих векторов будет отличен от нуля

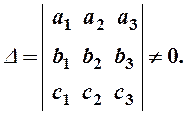                                                    (1)

В этом случае любой вектор  можно представить в виде  где числа  являющиеся координатами вектора  в базисе векторов  найдутся из системы уравнений

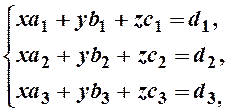                                                                       (2)

Пример.

Решение. Проверяем условие (1)

 

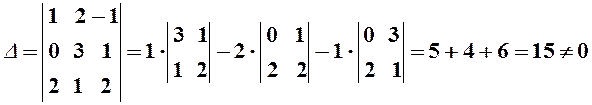
Таким образом векторы  образуют базис. Найдем теперь координаты вектора  в этом базисе. Запишем систему (2)

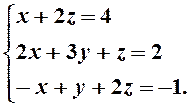
Решим эту систему по формулам Крамера

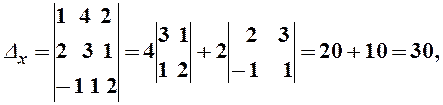
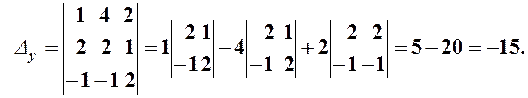
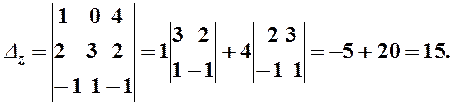
Отсюда

Ответ:

Задание 2  Даны координаты вершин пирамиды А₁,А_2,А₃,А₄. Найти : 1) длину ребра А₁А₂; 2) угол между ребрами А₁А₂ и А₁А₄; 3) угол между ребром А₁А₄ и гранью А₁А₂А₃;  4)площадь грани А₁А₂А₃; 5)объем пирамиды;  6) уравнение прямой А₁А₂;  7) уравнение плоскости А₁А₂А₃;  8) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертеж.

Указания к решению. Пусть дано    тогда

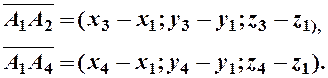
Длина вектора  найдется по формуле

                           (3)

Угол между ребрами А₁А₂ и А₁А₄ находится с помощью скалярного произведения

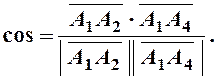                                                    (4)

Вектор, перпендикулярный грани А₁А₂А₃, определится через произведение векторов 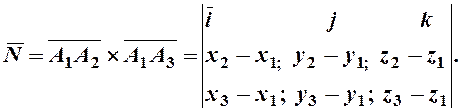(5)

Угол  между ребром А₁А₄ и гранью А₁А₂А₃  определится из формулы

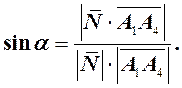                                                                                                                         (6)

Площадь грани А₁А₂ А₃:                                                 (7)

Объем пирамиды А₁А₂:                  (8)

Уравнение прямой А₁А₂: 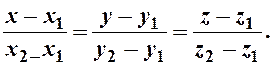                 (9)

Уравнение плоскости А₁А₂А₃:

     (10)

-координаты вектора    из (5)

Уравнение высоты из вершины А₄ на грань А₁А₂А₃:

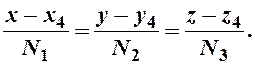                                                      (11)

Пример.  Дано  А₁(2;0;4), А₂(-1;3;2), А₃(5;6;-2), А₄(3;-1;1).  Решить задание 2.

Решение.

1)   Тогда из (3)

2) по формуле (4)

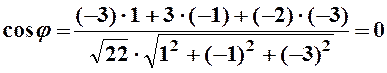, поэтому .

3) из (5)и (6) находим

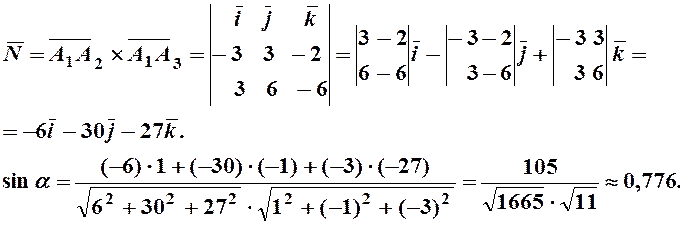
Отсюда .

4)Площадь грани А₁А₂А₃ определяем по (7) с учетом пункта 3) из этого задания

5)Объем пирамиды А₁А₂А₃А₄ находим по формуле (8)

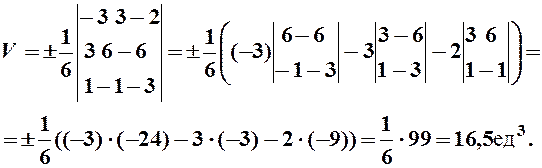
6)Уравнение прямой А₁А₂   (9)

7)Уравнение плоскости А₁А₂А₃ определяем по (10)

 

или, раскрывая скобки, : 

8)Уравнение высоты из вершины А₄ на грань А₁А₂А₃

      Задание 3. Линия задана уравнением  в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от j=0 до j=2p,  придавая  j  значения через промежуток ;

2) Найти уравнение этой линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной полуосью; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

 Указания к решению. Полярная система координат состоит из фиксированной точки – начала системы координат и луча, исходящего из этой точки – полярной оси. Если r>0, то точку М, имеющую полярные координаты (r, j), следует откладывать вдоль луча, образующего угол j с полярной осью на расстоянии r  от начала координат, , а если r<0, то точку М(r, j) следует откладывать на продолжении луча в противоположную сторону относительно начала координат.

Для перехода от задания линии в полярной системе координат к заданию этой линии в декартовой системе, необходимо воспользоваться следующими формулами перехода:

 (12)

Пример.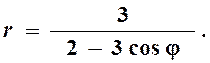   

Составим таблицу для значений r

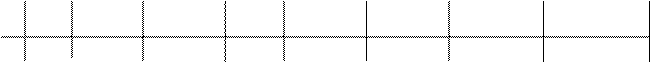
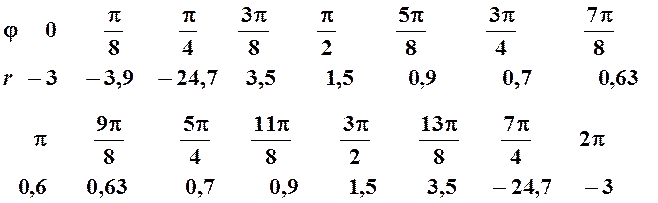
Проведем построение линии по данным таблицы

 

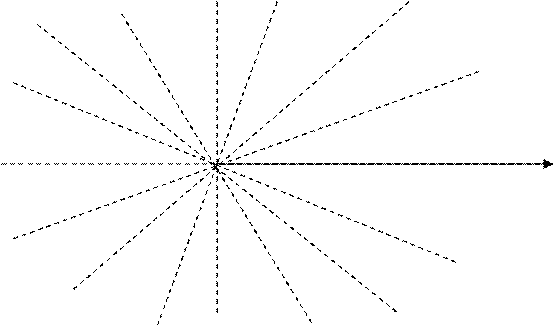Найдем теперь уравнение данной линии в декартовой системе координат. Перепишем сначала его в виде

Последнее уравнение с учетом формул перехода от декартовой системы координат к полярной примет вид

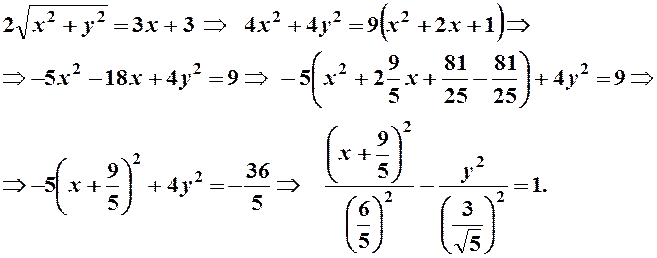
Последнее уравнение есть каноническое уравнение гиперболы с центром в точке 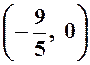   и полуосями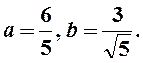 

Задание 4.  Дана система линейных уравнений

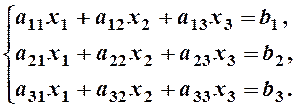                           (13)

Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

Указания к решению. Система имеет единственное решение, если определитель, составленный из коэффициентов системы, отличен от нуля

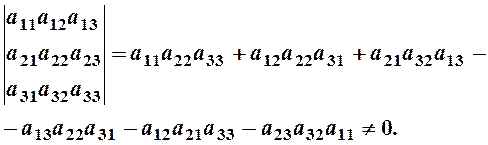
1). Метод Гаусса состоит в последовательном исключении неизвестных из уравнений с помощью сложения и вычитания уравнений, входящих в систему. При этом обычно пользуются только матрицей при неизвестных и столбцом свободных членов в виде

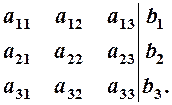                                     (14)

Первый шаг состоит в приведении коэффициента при  в первом уравнении к 1. Для этого первую строку в (14) необходимо разделить на   :

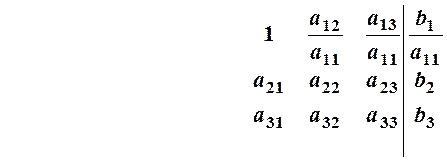                                  (15)

Второй шаг состоит в приведении коэффициентов при  во втором и третьем уравнениях к нулю. Для этого первую строку в (15) умножаем на (- и прибавляем ко второй