















В лекции 15 было показано, что при анализе процессов в синхронной
машине, работающей в режиме вентильного двигателя, ее можно представить в виде двухфазной
модели во вращающейся с синхронной скоростью системе координат d-q. В такой
координатной системе реальные обмотки статора с приложенными к ним
синусоидальными напряжениями заменяются двумя расположенными по осям d и q и
вращающимися вместе с ними обмотками, к которым приложены напряжения ![]() и
и
![]() ,
представляющие собой проекции обобщенного вектора напряжения
,
представляющие собой проекции обобщенного вектора напряжения ![]() на
эти оси. Поскольку ротор двигателя вращается в пространстве с угловой скоростью
на
эти оси. Поскольку ротор двигателя вращается в пространстве с угловой скоростью
![]() ,
напряжение возбуждения
,
напряжение возбуждения ![]() ,
представляющее собой напряжение постоянного тока, и ток возбуждения
,
представляющее собой напряжение постоянного тока, и ток возбуждения ![]() можно
рассматривать как вращающиеся в пространстве обобщенные вектора, направленные
по оси d, т.е. имеющие проекции только на ось d:
можно
рассматривать как вращающиеся в пространстве обобщенные вектора, направленные
по оси d, т.е. имеющие проекции только на ось d:
![]()
![]() .
.
С учетом того,
что частота роторной ЭДС равна нулю, ![]() ,
уравнения ((1)Л.15) для неявнополюсной машины примут вид:
,
уравнения ((1)Л.15) для неявнополюсной машины примут вид:
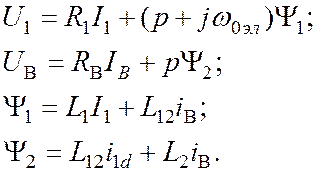 (1)
(1)
Подставляя ![]() из
третьего уравнения в первое, можно записать выражение для обобщенного вектора
напряжения на статоре в виде:
из
третьего уравнения в первое, можно записать выражение для обобщенного вектора
напряжения на статоре в виде:
![]() .
.
В статическом
режиме, имея в виду, что входящее сюда выражение ![]() представляет
собой сдвинутый на
представляет
собой сдвинутый на ![]() относительно
тока
относительно
тока ![]() вектор
ЭДС, наводимой в обмотках статора потоком ротора, получим:
вектор
ЭДС, наводимой в обмотках статора потоком ротора, получим:
![]()
![]() .
.
Учитывая, что
![]()
![]()
![]() ,
а
,
а ![]() ,
систему равенств (1) можно записать в виде: проекций на оси вращающейся системы
координат:
,
систему равенств (1) можно записать в виде: проекций на оси вращающейся системы
координат:
![]()
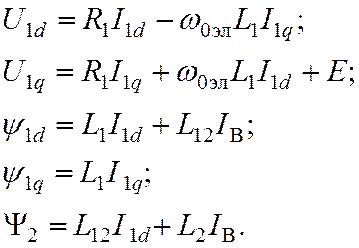 (2)
(2)
Определив ![]() или
или
![]()
(так как ![]() )
и подставив это в третье уравнение, можно с учетом пятого равенства установить
связь между
)
и подставив это в третье уравнение, можно с учетом пятого равенства установить
связь между ![]() и
проекцией вектора потокосцепления статора на ось d:
и
проекцией вектора потокосцепления статора на ось d:
![]() (3)
(3)
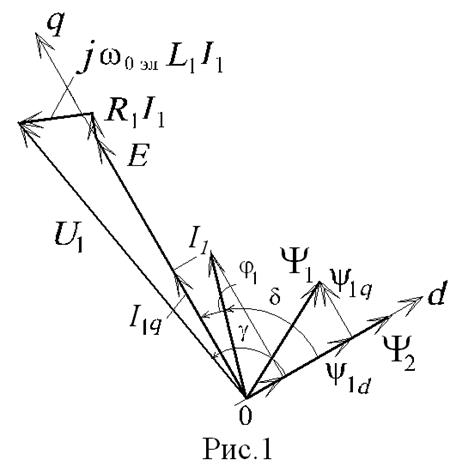
На основании
приведенных выражений, в предположении, что составляющая тока ![]() положительна,
на рис.1 построена пространственная векторная диаграмма, на которой через
положительна,
на рис.1 построена пространственная векторная диаграмма, на которой через ![]() обозначен
угол между векторами
обозначен
угол между векторами ![]() и
и
![]() ,
отсчитываемый от оси d против
часовой стрелки.
,
отсчитываемый от оси d против
часовой стрелки.
На основании общей формулы для момента двигателя
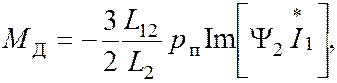 где
где
![]() -
мнимая часть произведения вектора потокосцепления ротора на комплексно-сопряженный
вектор тока статора, можно, обозначив
-
мнимая часть произведения вектора потокосцепления ротора на комплексно-сопряженный
вектор тока статора, можно, обозначив ![]() получить
получить
![]()
![]() или,
поскольку
или,
поскольку ![]()
![]()
Отсюда следует, что при данном значении потокосцепления
ротора требуемый момент двигателя будет обеспечиваться при минимальном значении
тока статора, если будет обеспечено равенство ![]() ,
т.е. составляющая тока статора по оси d будет равна нулю. Выражения (2) при этом приобретут
вид:
,
т.е. составляющая тока статора по оси d будет равна нулю. Выражения (2) при этом приобретут
вид:
![]()
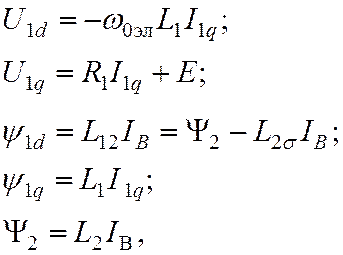 (4)
(4)
а формула для момента с учетом последнего равенства будет
![]()
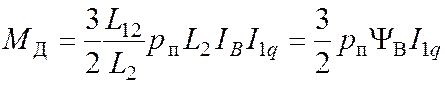 ,
,
 где обозначено
где обозначено ![]() -
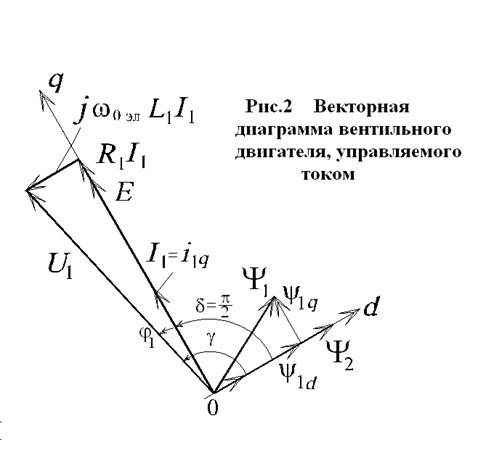
потокосцепление обмотки статора от тока возбуждения. Соответствующая векторная
диаграмма приведена на рис.2.
-
потокосцепление обмотки статора от тока возбуждения. Соответствующая векторная
диаграмма приведена на рис.2.
При задании
средствами системы управления вентильным двигателем угла ![]() угловой
сдвиг
угловой
сдвиг ![]() между
напряжением на статоре
между
напряжением на статоре ![]() и
током статора
и
током статора ![]() ,
как следует из рис.2, следующим образом связан со значениями частоты напряжения
питания и тока статора:
,
как следует из рис.2, следующим образом связан со значениями частоты напряжения
питания и тока статора:
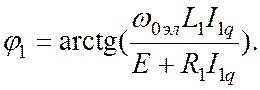 (5)
(5)
В режиме идеального холостого хода ток статора равен нулю, а вектор ЭДС совпадает с вектором приложенного напряжения.
Равенство ![]() может
быть непосредственно обеспечено при управлении током статора двигателя. При
этом задача управления вентильным двигателем состоит в том, чтобы для каждого
мгновенного значения угла поворота ротора (оси d ) относительно статора (неподвижной системы координат x-y) формировать
мгновенные значения токов фаз двигателя так, чтобы угол
может
быть непосредственно обеспечено при управлении током статора двигателя. При
этом задача управления вентильным двигателем состоит в том, чтобы для каждого
мгновенного значения угла поворота ротора (оси d ) относительно статора (неподвижной системы координат x-y) формировать
мгновенные значения токов фаз двигателя так, чтобы угол ![]() между
векторами
между
векторами ![]() и
и
![]() был
равен 90°.
был
равен 90°.
Другим способом
управления является управление статорным напряжением, при котором, в отличие от
предыдущего случая, формируются мгновенные значения фазных напряжений. Если при
этом поддерживать равным 90°
угол между ![]() и
и
![]() (
(![]() ,
то в системе уравнений (1) изменится первое выражение, которое запишется в
виде:
,
то в системе уравнений (1) изменится первое выражение, которое запишется в
виде:
![]() .
(6)
.
(6)
 Связь между
Связь между ![]() и
и
![]() определяется
равенством (3).
определяется
равенством (3).
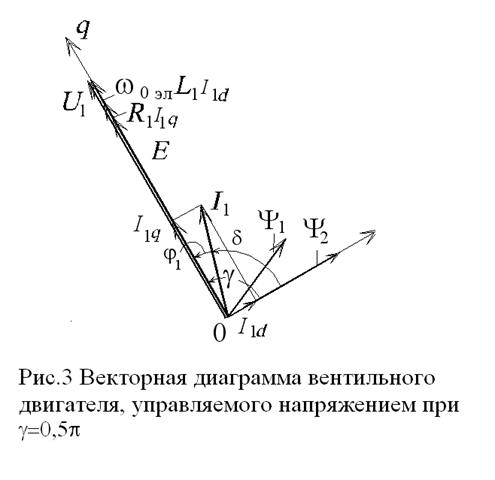
Этому соответствует
векторная диаграмма рис.3. На ней ток статора показан отстающим от напряжения ![]() на
угол
на
угол ![]() ,
который с учетом выражения (6) определится как
,
который с учетом выражения (6) определится как
![]()
![]() =
=![]() .
.
При этом угол между ![]() и
и
![]() будет
равен
будет
равен ![]() .
Значение этого угла определяет отклонение рассматриваемого режима работы от
оптимального, которым является режим при
.
Значение этого угла определяет отклонение рассматриваемого режима работы от
оптимального, которым является режим при ![]() и
и
![]()
Для того
чтобы при управлении напряжением реализовать режим работы двигателя с ![]() ,
что соответствует векторной диаграмме рис.2, нужно обеспечить сдвиг вектора
,
что соответствует векторной диаграмме рис.2, нужно обеспечить сдвиг вектора ![]() относительно
оси d на угол
относительно
оси d на угол ![]() (см.
рис.2), который с учетом (5) определится как
(см.
рис.2), который с учетом (5) определится как
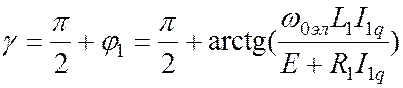 .
.
Сделать это
достаточно сложно, поскольку угол является функцией скорости (частоты) и
момента нагрузки двигателя. Задача упрощается, если двигатель предназначен для
работы на низких скоростях, когда можно пренебречь ЭДС вращения, положив с
определенной степенью приближения E=0. Тогда
требуемый сдвиг напряжения относительно оси d может быть определен как ![]() .
При малых значениях
.
При малых значениях ![]() выполняется
неравенство
выполняется
неравенство ![]() и
и
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.